علاقهمندان به مباحث مختلف طراحی الگوریتم و همینطور شرکتکنندگان مسابقات برنامهنویسی به خوبی میدانند که یکی از مهمترین پارامترهای طراحی موفقیتآمیز یک الگوریتم، شیوه صحیح فکر کردن روی حل مسئله است. حل انواع سوالات الگوریتمی به ما کمک میکند ذهن خودمان را برای حل مسائل پیچیدهتر آماده کنیم. مسئله برج هانوی (Tower of Hanoi) یکی از مسائل تاریخی مشهور است که در مباحث طراحی الگوریتم نیز به آن پرداخته میشود.
به شکل زیر توجه کنید.

سه میله - میله مبدأ (A) ، میله کمکی (B) و میله مقصد (C) - و تعدادی دیسک در میله مبدأ داریم. هدف انتقال تمام دیسکها از این میله به میله مقصد با رعایت دو شرط زیر است.
به طور حتم میتوان با روش آزمون و خطا به نتیجه مطلوب رسید. اما هدف ما ارائه الگوریتمی برای انتقال دیسکها با کمترین جابجایی ممکن است.
به عنوان مثال، اگر $ n = 2 $ باشد:
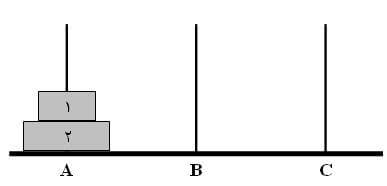
1) دیسک 1 را به میله B منتقل میکنیم $ (A \rightarrow B) $:
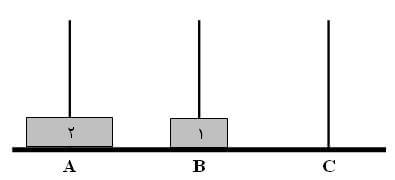
2) دیسک 2 را به میله C منتقل میکنیم $(A \rightarrow C)$:
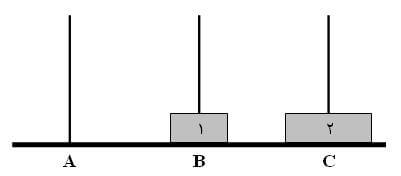
3) دیسک 1 را به میله C منتقل میکنیم $(B \rightarrow C)$:
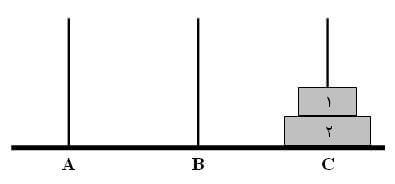
توجه داشته باشید که بر اساس قانون اول، نمیتوان به غیر از بالاترین دیسک هر میله، به دیسک دیگری از آن دسترسی پیدا کرد.
[برگرد بالا]
برای اینکه بتوان از روش بازگشتی تقسیم و حل (یا تقسیم و غلبه - Divide and Conquer) برای حل یک مسئله استفاده نمود، مسئله باید قابلیت خرد شدن به زیرمسئلههایی از همان نوع مسئله اصلی و اندازه کوچکتر را داشته باشد. این ویژگی در مورد مسئله برج هانوی صدق میکند.
ایده اصلی از آنجا ناشی میشود که برای جابجا کردن بزرگترین دیسک از میله A به میله C، ابتدا باید تمامی دیسکهای کوچکتر به میله B منتقل شوند. پس از تمام شدن این مرحله، دیسک بزرگ را از میله A به میله C منتقل کرده و مجددا به کمک میله A تمامی دیسکهای میله B را به میله C منتقل میکنیم. پس به طور خلاصه میتوان گفت:
مرحله یک: $n - 1$ دیسک بالایی میله مبدأ با شرایط ذکر شده و به کمک میله C به میله B منتقل میشوند.
مرحله دو: بزرگترین دیسک از میله مبدأ به میله مقصد منتقل میشود.
مرحله سه: $n - 1$ دیسک میله B با کمک گرفتن از میله A به میله مقصد منتقل میشوند.
میبینیم که توانستیم عملیات جابجا کردن $n$ دیسک را به دو عملیات مشابه ولی با اندازه کمتر و یک عملیات ساده تقسیم کنیم.
تابع بازگشتی زیر به زبان ++C ترتیب حرکتها را چاپ میکند:
void hanoi(int nDisk, char start, char temp, char target){
if(nDisk == 0)
return;
hanoi(nDisk - 1, start, target, temp);
cout << start << " -> " << target<< endl;
hanoi(nDisk - 1, temp, start, target);
}
برای مثال، فراخوانی تابع به صورت ('hanoi(3, ‘A’, ‘B’, ‘C، مسئله برج هانوی را با سه دیسک که در میله A قرار دارند و با کمک میله B به میله C منتقل خواهند شد، حل میکند. به همین ترتیب کد زیر پیادهسازی الگوریتم با زبان برنامهنویسی پایتون است.
def Hanoi(nDisk: int, start: str, temp: str, target: str):
if nDisk == 0:
return
Hanoi(nDisk - 1, start, target, temp)
print(start, '->', target)
Hanoi(nDisk - 1, temp, start, target)
واضح است که تابع بازگشتی فوق کمترین تعداد حرکت را چاپ میکند. چرا که برای جابجا کردن بزرگترین دیسک از پایین میله A، بقیه دیسکها باید در میله B باشند. فقط در این صورت این دیسک جابجا میشود. در فراخوانیهای بعدی، دیسک دوم از نظر بزرگی جابجا میشود و الی آخر. پس در این فراخوانیها جابجایی بیهودهای صورت نمیگیرد. نیز توالی حرکتها برای هر $n$ منحصر بفرد است. یعنی برای یک $n$ مشخص، دو توالی متمایز از جابجاییها وجود ندارد که تعداد جابجایی آنها کمتر یا مساوی این حالت باشد.
[برگرد بالا]
در حالت کلی میخواهیم بدانیم اگر تعداد دیسکها $n$ باشد، کمترین تعداد حرکت برای جابجا نمودن دیسکها چقدر است؟
فرض کنید $ T(n) $ تعداد حرکتهای لازم جهت انتقال $n$ دیسک به مقصد باشد. بر اساس توضیحات فوق، تعداد $T(n - 1)$ حرکت برای انتقال $n - 1$ دیسک به میله کمکی، یک حرکت برای انتقال بزرگترین دیسک به میله مقصد و مجددا $ T(n - 1) $ حرکت برای انتقال $n - 1$ دیسک موجود در میله کمکی به میله مقصد نیاز است. پس:
\[T(n) = 2 T(n - 1) + 1 \]
با حل این رابطه بازگشتی به روشهای ریاضی، به نتیجه زیر میرسیم:
\[T(n) = 2^n - 1 \]
مرتبه اجرایی این الگوریتم $ O(2^n) $ است که چندان مرتبه مطلوبی به نظر نمیرسد. اما همانگونه که بحث شد، این روش حداقل تعداد حرکتهای ممکن را میدهد؛ و هرگز نمیتوان روش دیگری با مرتبه پایینتر برای حل آن یافت.
[برگرد بالا]
مسئله برج هانوی علاوه بر روش تابع بازگشتی، راه حلهای غیربازگشتی نیز دارد. تا به اینجا مشخص شده است که بهترین راه حل برای جابجا کردن $n$ دیسک، به تعداد نمایی حرکت نیاز دارد. در نتیجه مرتبه راه حلهای آن در بهینهترین حالت - چه بازگشتی و چه غیربازگشتی - از مرتبه $ 2 ^n $ خواهد بود. اما آنچه که راه حل بازگشتی و غیربازگشتی را از هم متمایز میکند، مرتبه فضای مصرفی آن است.
حل بازگشتی مسئله، فراخوانیهای تو در تو و فضای پشته از مرتبه $ O(n) $ نیاز دارد. در حالی که میتوان با استفاده از روش غیربازگشتی این مرتبه را به $ O(1) $ کاهش داد. البته این مسئله تنها دلیل بررسی روش غیربازگشتی نیست. تبدیل مرتبه مصرف فضا از $ O(n) $ به $ O(1) $ زمانی که مرتبه اجرای الگوریتم $ O(2 ^ n) $ است، چندان قابل توجه نیست. دلیل دیگر میتواند این باشد که برخی زبانهای برنامهنویسی از فراخوانی بازگشتی توابع پشتیبانی نمیکنند و مجبور به استفاده ار روشهای غیربازگشتی هستند. اما دلیل اصلی این است که با بررسی این روشها، تمرین کوچکی برای تبدیل الگوریتمهای بازگشتی به غیربازگشتی انجام میدهیم.
تا کنون چندین روش مختلف جهت پیادهسازی غیربازگشتی حل مسئله برج هانوی ارائه شده است که در اینجا دو روش معرفی میشود. توجه داشته باشید که همه جزئیات حل مسئله به صورت دقیق و مشروح مطرح نمیشود و استدلال قسمتی از نتیجهگیریها به عنوان تمرین به خواننده واگذار میگردد.
روش اول- حل مسئله برج هانوی را میتوان معادل پاسخ دادن به این سوال دانست که: در هر مرحله کدام دیسک به کدام میله منتقل میشود؟
سوال اول: کدام دیسک؟ فرض کنیم دیسکهایی به شعاع $y$، $x$ و $z$ که رابطه $ x < y < z $ را با هم دارند، کوچکترین دیسک هر میله باشند. به عبارت دیگر، این سه دیسک بالاترین دیسکهای میلهها هستند که قابلیت جابجایی دارند. اگر میلهای شامل هیچ دیسکی نباشد، دیسکی با شعاع بینهایت را برای آن در نظر میگیریم. حال به استدلالهای منطقی زیر توجه کنید:
استدلال شماره 1) $x$ برابر 1 است. چرا که بر اساس قوانین حاکم بر مسئله، هیچ دیسکی نمیتواند روی دیسک 1 قرار بگیرد. در نتیجه این دیسک همیشه بالاترین دیسک موجود در یکی از میلهها است.
استدلال شماره 2) در آغاز همه دیسکها روی یک میله قرار دارند که دیسک 1 بالاترین دیسک آن است. پس در اولین مرحله دیسک 1 جابجا میشود.
استدلال شماره 3) دیسکهایی که طی دو مرحله متوالی جابجا میشوند حتما متمایز هستند. این مسئله از بهینه بودن راه حل ناشی میشود. اگر قرار باشد طی دو مرحله متوالی یک دیسک خاص را جابجا کنیم، میتوانیم دو مرحله را با هم ادغام کرده و کل جابجایی را یکجا انجام دهیم.
استدلال شماره 4) با توجه به قوانین حاکم بر مسئله، دیسک $z$ نمیتواند حرکت کند. چرا که دیسکهای $x$ و $y$ هر دو از آن کوچکتر هستند.
استدلال شماره 2 میگوید که اولین حرکت همیشه با دیسک 1 است. استدلال شماره 3 میگوید حرکت بعدی با دیسکی غیر از دیسک 1 است. استدلال شماره 4 میگوید این دیسک نمیتواند بزرگترین دیسک موجود در بالای میلهها باشد. پس در مرحله بعدی دیسک $y$ جابجا خواهد شد. و بالاخره حرکت بعدی باز هم با دیسک 1 است (چرا؟).
پس با بررسی منطقی خود به این نتیجه رسیدیم که دیسک 1 و دیسکی که بزرگترین دیسک در آن مرحله نیست، به صورت متناوب جابجا میشوند. مراحل با شماره فرد برای دیسک 1 و مراحل با شماره زوج برای دیسک y.
سوال دوم: کدام میله؟ حال که میدانیم در هر مرحله کدام دیسک جابجا میشود، به سراغ میله مقصد میرویم. در مراحل زوج که دیسک $y$ منتقل خواهد شد، تشخیص میله مقصد بسیار آسان است. چرا که روی یکی از میلهها دیسک 1 قرار دارد که دیسک $y$ نمیتواند روی آن قرار بگیرد. در نتیجه به تنها میله باقیمانده (میله دیسک $z$) منتقل میشود. در مورد مراحلی هم که دیسک 1 قرار است جابجا شود، میتوان اینطور استدلال کرد:
فرض کنیم دیسک 1 روی میله A قرار داشته باشد و آن را به میله C منتقل کنیم. در مرحله بعدی دیسک y جابجا میشود. و در مرحله بعد باز هم دیسک 1 باید جابجا شود. حال اگر این دیسک را به میله A بازگردانیم، به نوعی کار اضافی و بازگشت به عقب انجام دادهایم. برای آشکار شدن این موضوع کافی است مسئله برج هانوی را با دو دیسک حل کنید و در حرکت دوم دیسک 1، آن را به میلهای بازگردانید که از آن آمده بود. پس میتوان گفت: در حرکتهای متوالی، دیسک شماره 1 به میلهای حرکت میکند که از آن به میله فعلی خود نیامده است. این مسئله نه تنها در مورد دیسک 1 که در مورد همه دیسکها صادق است. یعنی همه دیسکها در حرکتهای خود به سمت میلهای میروند که در حرکت قبلی خود از آن نیامدهاند. اما لحاظ کردن این شرط برای این دیسکها لازم نیست. چرا که در هر مرحله، تنها یک انتخاب برای حرکت خود دارند.
تنها مسئله باقیمانده، میله مقصد دیسک 1 در اولین حرکت خود است. زمانی که این دیسک اولین حرکت خود را انجام میدهد، نمیتوان از استدلال فوق برای تشخیص میله مقصد استفاده کرد (چرا؟). استدلال این قسمت را هم که چندان دشوار نیست به شما وا میگذارم و تنها به بیان نتیجه میپردازم: اگر تعداد دیسکها زوج باشد، دیسک 1 را در اولین حرکت به میله کمکی (یعنی میله B) و در غیر اینصورت به میله مقصد (یعنی میله C) منتقل میکنیم.
به این ترتیب حل مسئله برج هانوی به صورت غیربازگشتی پیادهسازی میشود. حال میدانیم که در هر مرحله کدام دیسک به کدام میله منتقل میشود.
روش دوم: یکی دیگر از روشهای پیادهسازی غیربازگشتی حل مسئله برج هانوی که در یک منبع اینترنتی مشاهده کردم، از الگوریتم زیر تبعیت میکند:
void hanoi(int nDisk, char start, char temp, char finish){
int max = nDisk;
char dest = finish;
int disk = max;
while(true){
while(disk > 0){
if(moving disk succeeds)
{
if(disk == max){
max--;
if(max == 0)
return;
}
dest = the final place of max;
}
else
dest = the alternative place between dest and the current place of disk;
disk--;
}
p and q = the places different of dest;
disk = the smaller of the disks on top of p and q;
dest = the place between p and q with greater disk on top;
}
}
تشریح عملکرد این الگوریتم یک تمرین خوب است. توضیح اینکه این الگوریتم بر خلاف الگوریتم قبلی که سعی در یافتن قوانین حرکت دیسکها داشت، دقیقا همان روش بازگشتی را شبیهسازی میکند.
در پایان توجه داشته باشید که دو روش ذکر شده، تنها روشهای پیادهسازی غیربازگشتی حل مسئله نیستند.