الگوریتم جستجوی اول عمق (Depth First Search - DFS) یا نامهای دیگری همچون جستجو در عمق، پیمایش اول عمق، پیمایش عمق اول الگوریتمی مشابه الگوریتم جستجوی اول سطح (BFS) برای پیمایش گراف است. این دو الگوریتم خواص و کاربردهای مشترک بسیاری دارند و تفاوت اصلی در این است که در هر تکرار الگوریتم DFS تنها یکی از گرههای مجاور گره پردازش شده برای مرحله بعد انتخاب میشود. به این ترتیب، الگوریتم DFS به جای صف از یک پشته برای مشخص کردن مسیر پیمایش استفاده میکند.
الگوریتم DFS با فرض انتخاب گره مبدأ به عنوان گره جاری از مراحل زیر تشکیل یافته است:
1- گره جاری را به پشته اضافه کن.
2- گره جاری را پردازش کن.
3- از گرههای مجاور گره جاری یک گره پیمایش نشده را به عنوان گره جاری انتخاب کرده و برو به مرحله 1.
4- اگر همه گرههای مجاور گره جاری پیمایش شدهاند، گره بالای پشته را به عنوان گره جاری از پشته حذف کرده و برو به مرحله 3.
5- اگر گرهی در پشته وجود ندارد، اجرای الگوریتم را متوقف کن.
منظور از پردازش، هر عملی روی گره است که پیمایش یا جستجو به آن نیت صورت گرفته است.
به عنوان مثال در گراف زیر:
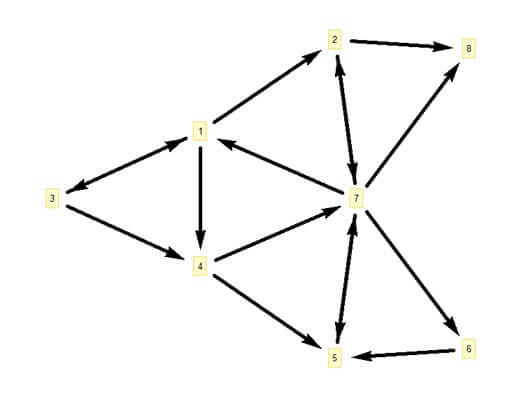
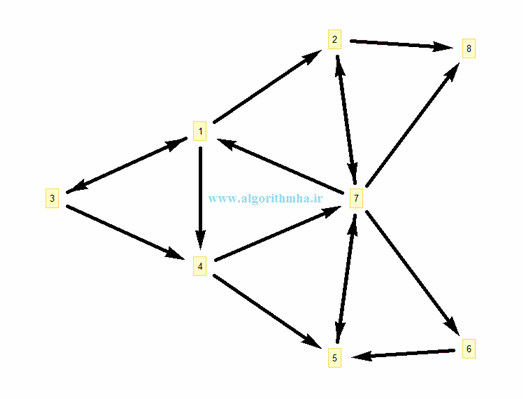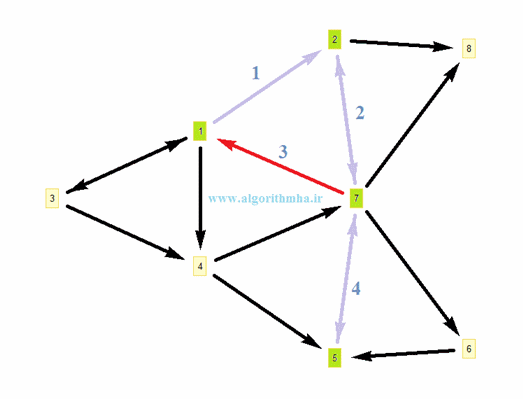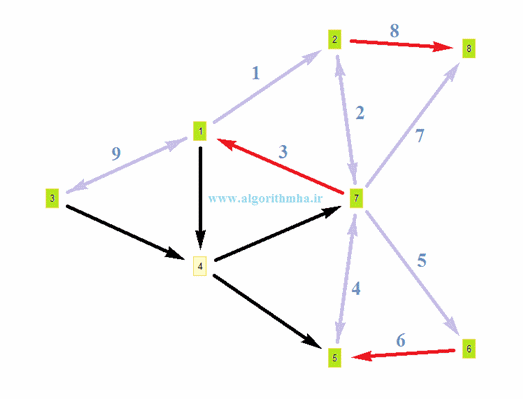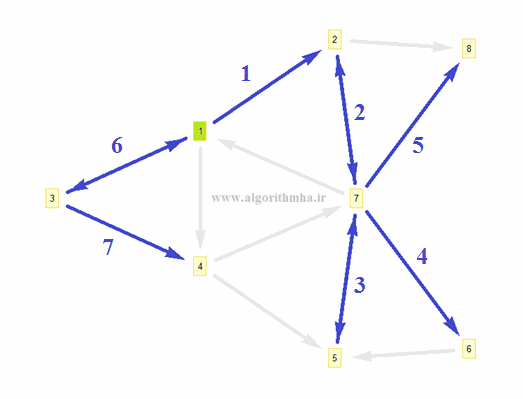
ترتیب پیمایش گرهها با شروع از گره شماره 1 به این ترتیب خواهد بود:
1, 2, 7, 5, 6, 8, 3, 4
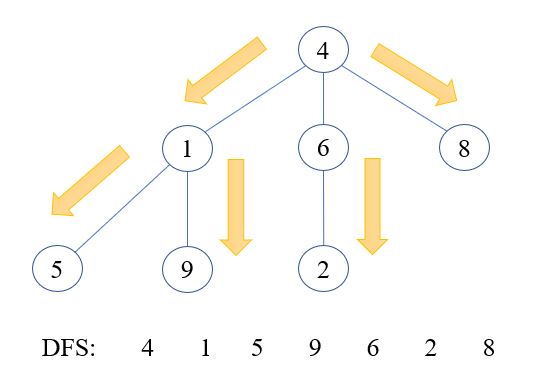
دلیل نامگذاری این روش با عبارت "اول عمق" در پیمایش یک درخت از ریشه مشخص میشود که گرهها به صورت عمقی پیمایش میشوند و اولویت پیمایش در حرکت به سمت عمق است.
پیادهسازی الگوریتم جستجوی اول عمق
تابع dfs یک پیادهسازی ساده از الگوریتم DFS به زبان برنامهنویسی ++C است که با دریافت مشخصات گراف، شماره اندیس گره جاری و لیستی از گرههای پیمایش شده، گراف را به صورت بازگشتی پیمایش کرده و شماره عدد هر گره را به عنوان پردازش آن چاپ میکند:
void dfs(int graph[MAX][MAX], bool visited[MAX], int numberOfNodes, int sourceNode){
cout << sourceNode + 1 << "\t" << endl;
visited[sourceNode] = true;
for(int i = 0 ; i < numberOfNodes ; i++)
if(graph[sourceNode][i] < INT_MAX && !visited[i])
dfs(graph, visited, numberOfNodes, i);
}
در این تابع از آرایه visited برای تشخیص گرههای پیمایش شده استفاده شده و فرض بر استفاده از INT_MAX برای مشخص کردن نبود یال بین دو گره است. حلقه for کار بررسی گرههای مجاور برای یافتن گره پیمایش نشده را بر عهده دارد. اگر چنین گرهی یافت شود، تابع به صورت بازگشتی برای پیمایش آن گره فراخوانی میگردد. در صورتی که هیچ گرهی یافت نشود، دستور فراخوانی بازگشتی داخل شرط if هرگز اجرا نشده و اجرای تابع بدون فراخوانی بازگشتی به پایان میرسد.
تذکر: تابع dfs از فراخوانی بازگشتی برای پیمایش استفاده میکند. در زمان اجرای این تابع، سیستم عامل اطلاعات فراخوانیهای بازگشتی را در یک پشته ذخیره میکند. بنابراین ساده بودن این قطعه کد دلیل بر عدم استفاده از پشته یا بهینه بودن آن، نسبت به زمانی که مدیریت پشته در خود کد برنامهنویسی شده باشد، نیست.
[برگرد بالا]
مرتبه زمانی اجرای الگوریتم جستجوی اول عمق برای گراف $ G = (V, E) $ برابر $O(\vert V \vert + \vert E \vert) $ است؛ چرا که این الگوریتم در بزرگترین حالت تمامی گرهها را پیمایش کرده و نیاز به بررسی تمامی یالها دارد. این مرتبه اجرایی در یک گراف همبند به صورت $ O(\vert E \vert) $ بوده (چرا؟) و در حالت کلی متناسب با تعداد یالها حداکثر از مرتبه $ O(n^2) $ است.

[برگرد بالا]
الگوریتم DFS و روش پیمایش آن کاربردهای فراوانی دارد که در ادامه به چند مورد مهم اشاره میشود.
1- تشخیص وجود مسیر: با استفاده از الگوریتم dfs میتوان وجود مسیر از گره مبدأ به گره دیگر را بررسی کرد.
نکته: اگر گراف همبند و بدون جهت باشد همواره مسیر بین هر دو گره دلخواه وجود دارد و نیاز به استفاده از این الگوریتم نیست.
تذکر: در الگوریتم BFS اگر گراف بدون وزن باشد، مسیر مشخص شده توسط الگوریتم به طور حتم کوتاهترین مسیر از گره مبدأ به مقصد است؛ اما در مورد الگوریتم DFS این خاصیت لزوما برقرار نیست.
2- تولید درخت پوشا: خروجی الگوریتم DFS روی یک گراف بدون جهت و همبند یک درخت پوشا است. در مورد گرافهای جهتدار ممکن است متناسب با گره مبدأ چنین درختی ساخته شود یا نشود.
3- تشخیص دور در گراف: اگر در حین پیمایش گراف، یکی از گزینههای پیمایش گرهی باشد که قبلا پیمایش شده است، به معنی وجود دور در گراف است.
نکته: اگر در یک گراف بدون جهت بیش از $ \vert V \vert - 1 $ یال وجود داشته باشد، گراف به طور حتم دور دارد (چرا؟).
4- تشخیص دو بخشی بودن گراف: یک گراف دوبخشی است اگر و فقط اگر بتوان گرههای آن را با استفاده از دو رنگ به نحوی نشانهگذاری کرد که هیچ دو گره مجاوری همرنگ نباشند. برای تشخیص دوبخشی بودن گراف با استفاده از الگوریتم DFS، هر گره در پیمایش با رنگ مخالف گره پیشین نشانهگذاری شده و بررسی میگردد که آیا از گرههای پیمایششده مجاورش گرهی با همین رنگ نشانهگذاری شده است یا نه. اگر چنین گرهی یافت شود به معنی عدم امکان رنگ شدن گراف با دو رنگ و در نتیجه دو بخشی نبودن گراف است. یافت نشدن چنین گرهی در هر مرحله تا انتهای اجرای الگوریتم به معنی دو بخشی بودن آن است که این دو بخش توسط رنگها متمایز شدهاند.
5- حل مارپیجهای تکمسیر: الگوریتم BFS راهکاری است که در یافتن کوتاهترین مسیر در مسیرهای مارپیچ (Maze) کاربرد دارد. اگر مسیر رسیدن به هر نقطه از مارپیچ یکی باشد (دوری در مارپیچ نباشد یا گراف معادل مارپیچ یک درخت باشد) میتوان از الگوریتم DFS نیز استفاده کرد. چرا که در چنین حالتی تنها یک مسیر به مقصد وجود داشته و کوتاه بودن آن مطرح نیست.