الگوریتمستان - درخت جستجوی دودویی

درخت دودویی (Binary Tree)

  [برگرد بالا]

درختی است که هر گره آن دارای حداکثر دو گره فرزند است که به آنها فرزند راست و چپ گره گفته می‌شود. به همین ترتیب زیردرختی که فرزند راست در رأس آن قرار دارد زیردرخت راست و زیردرختی که فرزند چپ در رأس آن قرار دارد زیردرخت چپ گره نامیده می‌شوند.

  

  

درخت جستجوی دودویی (Binary Search Tree - BST)

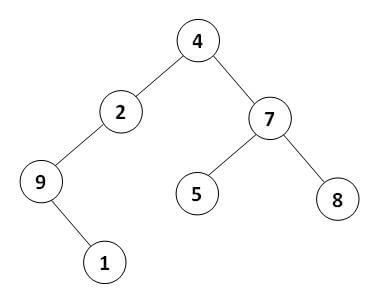
  [برگرد بالا]

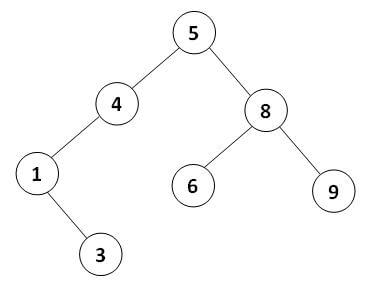
درختی دودویی است که برای هر گره آن شروط زیر برقرار هستند:

1- مقادیر تمامی گره‌های زیردرخت راست - در صورت وجود - از مقدار گره بزرگتر هستند.

2- مقادیر تمامی گره‌های زیردرخت چپ - در صورت وجود - از مقدار گره کوچکتر هستند.

با توجه به چنین تعریفی، واضح است که فرزندان چپ و راست یک گره در صورت وجود به ترتیب مقداری کمتر و بیشتر از مقدار خود گره دارند.

  

  

کاربرد درخت جستجوی دودویی

  [برگرد بالا]

مهمترین کاربرد چنین درختی از نام آن مشخص است. این درخت با توجه به تعریف آن برای انجام عملیات جستجو مناسب است. فرض کنید در مجموعه اعداد درخت فوق به دنبال عدد 6 هستیم. ابتدا 6 را با مقدار گره رأس - یعنی 5 - مقایسه می‌کنیم. این گره، گره مورد نظر ما نیست. عدد 6 هم از عدد 5 بزرگتر است. در نتیجه با توجه به تعریف درخت جستجوی دودویی، مطمئن هستیم که اگر گرهی با مقدار 6 وجود داشته باشد، به طور حتم در زیردرخت راست گره 5 است. پس به سمت راست حرکت کرده و عدد 6 را با 8 مقایسه می‌کنیم. باز هم به گره مطلوب نرسیدیم. اما با توجه به اینکه 6 از 8 کوچکتر است، به زیردرخت چپ گره 8 مراجعه می‌کنیم. در این مرحله به گره با مقدار 6 می‌رسیم که گره مطلوب ما است.

  

  

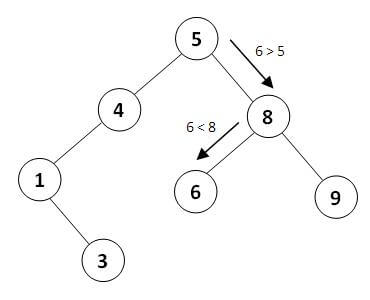
اگر در حین جستجو مجبور به حرکت به سمتی شدیم که زیردرختی وجود ندارد، به این معنی است که گره مورد نظر در درخت وجود ندارد.

  

  

تحلیل الگوریتم جستجوی درخت

  [برگرد بالا]

در جستجو با استفاده از درخت جستجوی دودویی، در هر مرحله اگر به گره مطلوب نرسیم، یک لایه در درخت به سمت پایین حرکت می‌کنیم. بنابراین تعداد مقایسه‌ها حداکثر برابر با عمق درخت است. حداقل تعداد مقایسه‌ها هم زمانی اتفاق می‌افتد که گره مورد نظر در رأس درخت قرار داشته باشد. در این حالت تنها یک مقایسه صورت می‌گیرد.

عمق یک درخت با $n$ گره حداکثر $n$ و حداقل $[log_2\;n]+1$ است (چرا؟). پس می‌توان گفت این روش جستجو حداقل از مرتبه یک، حداکثر از مرتبه $n$ و به طور متوسط از مرتبه $log\;n$ است.

  

نکته: در روش جستجوی دودویی در بدترین حالت هم مرتبه اجرا log n است. چرا که در هر مرحله به طور حتم داده‌ها به دو قسمت تقسیم می‌شوند. در نتیجه اگر یک درخت جستجوی دودویی و یک آرایه مرتب از مجموعه اعداد یکسان داشته باشیم، با صرفه‌تر است که از روش جستجوی دودویی برای جستجو استفاده کنیم. مگر آنکه درخت با توزیع مناسبی ساخته شده باشد و عمق آن حداقل باشد.

  

درج گره جدید در درخت جستجوی دودویی

  [برگرد بالا]

زمانی که اقدام به درج یک گره جدید ذر درخت جستجوی دودویی می‌کنیم، باید محل مناسبی برای این گره پیدا کنیم. برای یافتن محل مناسب، فرض می‌کنیم که چنین گرهی در درخت وجود دارد و عملیات جستجو را برای آن انجام می‌دهیم. در نهایت به طور حتم به گرهی خواهیم رسید که حداقل یکی از فرزندان آن تهی است (چرا؟). این گره والد گره جدید خواهد بود.

برای مثال فرض کنید می‌خواهیم گرهی با مقدار 7 را به درخت فوق اضافه کنیم:

  

  

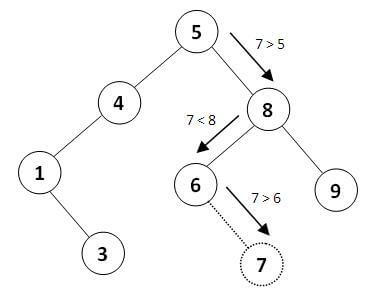
و اگر گرهی با مقدار صفر درج کنیم:

  

  

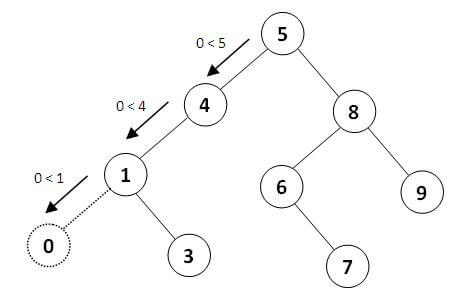
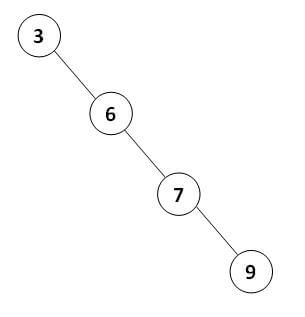
زمانی که قصد ساخت یک درخت جستجوی دودویی را داریم، ترتیب درج مقادیر تاثیر مستقیمی در عمق درخت و سرعت اجرای عملیات جستجو خواهد داشت. اگر مجموعه اعداد وارد شده از قبل مرتب باشند، درخت به دست آمده از عمق n خواهد بود که در هر لایه آن تنها یک گره وجود دارد:

  

  

بهترین حالت زمانی اتفاق می‌افتد که درخت ایجاد شده حداقل مقدار ممکن برای عمق ($log_2\;n] + 1]$) را داشته باشد. اما تشخیص چنین ترتیبی برای درج گره‌ها همواره آسان نیست. به همین خاطر روشهایی مانند AVL برای ساخت درخت‌ها ابداع شده است. درخت AVL درختی است که اختلاف عمق زیردرخت‌های چپ و راست هر گره، حداکثر یک است. برای ساختن چنین درختی از دستورالعمل خاصی استفاده می‌شود.

  

  

حذف گره از درخت جستجوی دودویی

  [برگرد بالا]

حذف گره از درخت جستجوی دودویی پیچیدگی‌هایی دارد که گاهی گره را تنها با علامت‌گذاری حذف می‌کنند. به عبارت دیگر در این حالت هر گره درخت شامل فیلدی است که وضعیت حذف آن را مشخص می‌کند. اگر گرهی را با استفاده از تغییر مقدار این فیلد حذف کنیم، در عمل حافظه آن آزاد نشده و تغییری در ساختار درخت ایجاد نمی‌شود. اما در پردازش‌های آتی، این گره را در نظر نمی‌گیریم. اما گاهی نیاز است که گره به طور کامل حذف شده و حافظه مصرفی آن نیز آزاد شود.

هر گره در درخت جستجوی دودویی ممکن است در یکی از سه وضعیت زیر باشد:

1- گره فاقد فرزند است: یعنی گره مذکور یک برگ است. در چنین حالتی به راحتی می‌توان گره را حذف کرده و فضای مصرفی آن را آزاد کرد.

  

  

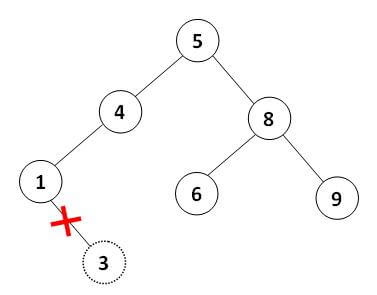
2- گره دارای یک فرزند است: در این حالت گره فرزند را جایگزین گره مذکور می‌کنیم. به عبارت ساده‌تر، بین والد گره و فرزند گره ارتباط مستقیم برقرار کرده و گره مطلوب را حذف می‌کنیم.

  

  

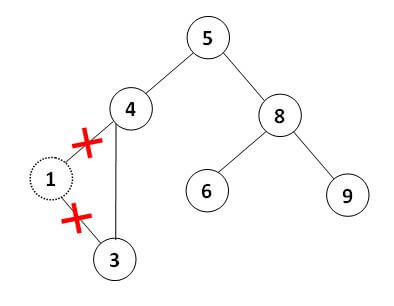
3- گره دارای دو فرزند است: این حالت کمی پیچیده‌تر از حالت‌های قبلی است. ابتدا گرهی با کوچک‌ترین مقدار در زیردرخت راست گره را پیدا می‌کنیم. درج این گره به جای گره قبلی شروط درخت جستجوی دودویی را به هم نمی‌زند (چرا؟). در نتیجه می‌توان به راحتی آن را جایگزین کرد.

  

  

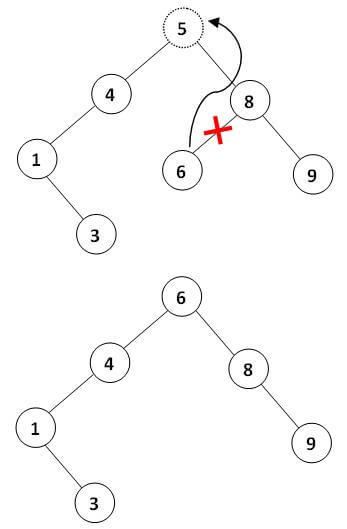
گرهی که جایگزین می‌شود به طور حتم فرزند چپ ندارد (چرا؟). اما ممکن است فرزند راست داشته باشد. در این حالت عمل حذف طی دو مرحله انجام می‌شود. ابتدا گره جایگزین از محل خود بنا به حالت شماره 2 حذف می‌شود. سپس گره اصلی با جایگزین شدن این گره حذف می‌گردد.

نکته: به کوچکترین گره زیردرخت راست گره، گره مابعد آن (Successor) گفته می‌شود. این نام‌گذاری به این خاطر است که اگر عناصر درخت با توجه به مقدار آنها مرتب شوند (مثلا با پیمایش Inorder) این گره بلافاصله بعد از آن قرار می‌گیرد. به همین ترتیب، گره ماقبل (Predecessor) یک گره نیز گرهی با بزرگترین مقدار در زیردرخت سمت چپ آن است. این گره نیز پس از مرتب‌سازی در کنار گره مفروض و قبل از آن قرار می‌گیرد. در حالت 3 برای حذف گره به جای عضو مابعد می‌توان از این گره نیز استفاده کرد.