صف اولویت‌دار (یا صف اولویتی - Priority Queue) از جمله ساختمان داده‌های بسیار پرکاربرد است. در صف عادی از تکنیک FIFO - مخفف First In First Out - استفاده می‌شود. در این تکنیک، مثل یک صف نانوایی، داده‌ها به ترتیب ورود پشت سر هم در صف قرار می‌گیرند. بنابراین اولین داده ورودی، اولین داده خروجی نیز خواهد بود. اما در صف اولویت‌دار برای هر داده، اولویتی - نه لزوما منحصربفرد - مشخص می‌شود. صف اولویت را می‌توان به اورژانس یک بیمارستان تشبیه کرد که هر بیمار با شدت بیماری بیشتر اولویت بیشتری برای رسیدگی دارد. سیستم عامل کامپیوتر هم برای مدیریت پردازش‌ها از صفهای اولویت‌دار استفاده می‌کند.
به عنوان مثال، فرض کنید پردازش‌های زیر در انتظار اختصاص CPU به خود هستند:
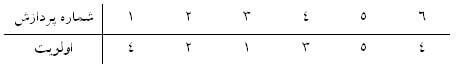
صف انتظار CPU یک صف اولویت‌دار است. در نتیجه CPU در اولین فرصت ممکن ابتدا پردازش شماره 3 را انجام می‌دهد. سپس پردازش شماره 2 و ...
تذکر: روش‌های زمان‌بندی CPU جهت انجام پردازش‌های مختلف یکی از بحث‌های جذاب و در عین حال مهم مبحث سیستم عامل است. بررسی تمامی روش‌های زمان‌بندی و مزایا و معایب آنها خارج از بحث فعلی ما است.
برای پیاده‌سازی صف اولویتی عموما از آرایه استفاده می‌شود. من در اینجا سه روش مختلف را شرح می‌دهم.
پیاده‌سازی با استفاده از آرایه نامرتب
[برگرد بالا]
در این روش زمانی که داده‌ای وارد صف می‌شود، همچون صف عادی در انتهای آن قرار می‌گیرد. به عنوان نمونه، داده‌های مثال زمان‌بندی CPU به صورت زیر در آرایه قرار می‌گیرند:
\
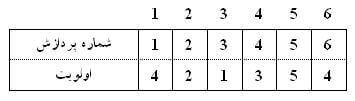
هر عنصر آرایه ساختمانی مرکب از دو عنصر شماره پردازش و اولویت آن است. هر پردازش جدید به انتهای صف اضافه می‌شود که از مرتبه $ O(1)$ است:
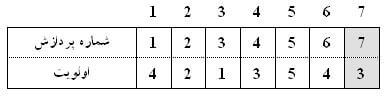
اما زمانی که قرار است پردازشی از آن خارج شود، باید تک تک عناصر بررسی شوند، تا پردازشی با بیشترین اولویت انتخاب شود. این فرآیند از مرتبه $ O(n)$ است.
پیاده‌سازی با استفاده از آرایه مرتب
[برگرد بالا]
در این روش بر خلاف روش قبل، آرایه بر اساس اولویت‌ها مرتب شده است.
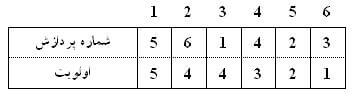
زمانی که داده‌ای وارد صف می‌شود، بر اساس اولویت خود در محل مناسب قرار می‌گیرد:
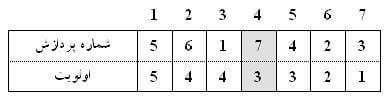
در این حالت پردازش با بیشترین اولویت همواره در انتهای صف قرار دارد و هزینه استخراج آن $ O(1)$ است. این مسئله در مقایسه با آرایه نامرتب یک برتری است. اما در این روش هزینه درج $ O(n)$ است که در مقایسه با روش قبلی بدتر است.
در کل می‌توان گفت روش آرایه مرتب و نامرتب هم‌ارز یکدیگر بوده و از لحاظ عملکرد تفاوت چندانی با هم ندارند.
پیاده‌سازی با استفاده از آرایه نیمه‌مرتب (درخت heap)
[برگرد بالا]
در این روش داده‌ها بر اساس اولویت آنها در یک درخت min-heap وارد می‌شوند:
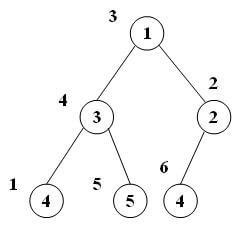
اعداد داخل گره‌ها اولویت و اعداد خارجی شماره پردازش هستند. درخت فوق در نمایش آرایه‌ای به این صورت خواهد شد:
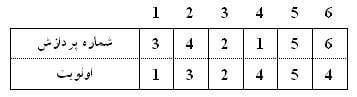
در یک درخت min-heap عنصری با کوچکترین کلید همواره در ریشه قرار دارد. در نتیجه عمل حذف گره ریشه از درخت min-heap، کوچکترین عنصر آن را به ما می‌دهد. این عمل بر اساس بحث‌های پیشین از مرتبه $ O(log\; n)$ است. عمل درج نیز در min-heap از همین مرتبه است.
عملیات درج و حذف روی یک صف اولویتی که با استفاده از آرایه مرتب یا نامرتب ساخته شده باشد، روی هم رفته از مرتبه اجرایی $n$ هستند. اما در روش آرایه نیمه‌مرتب این مرتبه به $log\; n$ کاهش میابد. پس می‌توان گفت که روش درخت هیپ برای پیاده‌سازی صف اولویتی کارآیی بسیار بهتری دارد.