مسئله ضرب زنجیرهای ماتریسها و پرانتزبندی بهینه آن یکی از مثالهای مشهور کاربرد برنامهنویسی پویا در حل مسائل بهینهسازی است.
فرض کنید قصد داریم حاصلضرب عبارت ماتریسی $ A_{3 \times 7} \times B_{7 \times 8 } \times C_{8 \times 4} $ را محاسبه کنیم. میدانیم که ضرب ماتریسها خاصیت شرکتپذیری داشته، اما خاصیت جابجایی ندارد. بنابراین رعایت ترتیب ضرب آنها مهم است. پرانتزبندیهای مختلف ضرب ماتریسها حالتهای مختلف محاسبه آن را به ما میدهند:
\[1: A \times (B \times C) \]
\[2: (A \times B) \times C \]
در حالت اول ابتدا B در C ضرب شده و سپس حاصل آنها در A ضرب میشود؛ و در حالت دوم ابتدا A و B در هم ضرب شده و سپس نتیجه در C ضرب میشود. حال سوال این است که آیا این پرانتزبندیها تفاوتی با هم دارند؟
ضرب ماتریس دلخواه $ M_{R \times L} $ در ماتریس دلخواه دیگری مانند $ N_{L \times C} $ به $ R \times L \times C $ عمل ضرب عددی نیاز دارد (چرا؟). با توجه به این موضوع، تعداد کل عملهای ضرب برای محاسبه حاصلضرب سه ماتریس فوق را در هر دو پرانتزبندی محاسبه میکنیم:
\[1: A \times (B \times C) : 7 \times 8 \times 4 + 3 \times 7 \times 4 = 308 \]
در حالت اول ابتدا ماتریس B در C ضرب میشود. سپس ماتریس A و ماتریس حاصل از ضرب اول، با ابعاد (4 ,7)، در هم ضرب میشوند. به همین ترتیب در مورد حالت دوم:
\[2: (A \times B) \times C : 3 \times 7 \times 8 + 3 \times 8 \times 4 = 264 \]
پس در پرانتزبندی به فرم دوم تعداد ضرب کمتری نیاز است.
ثابت شده است که تعداد کل حالتهای پرانتزبندی ضرب زنجیری n ماتریس، مطابق با جملات دنباله اعداد کاتالان هستند:
\[C_{n-1} = \frac{1}{n} \begin{pmatrix} 2n - 2 \\ n - 1 \end{pmatrix} \]
هدف ما این است که در بین تمامی این حالتها، حالتی را بیابیم که حاصلضرب ماتریسها با حداقل ضرب عددی محاسبه شود.
[برگرد بالا]
ابتدا سعی میکنیم با استفاده از روش تقسیم و حل الگوریتمی برای پاسخ مسئله پیدا کنیم. برای این کار عبارت مورد نظر را به دو قسمت تقسیم میکنیم. به عنوان مثال فرض کنید n = 7 باشد. در این صورت به شش طریق میتوان عبارت را به دو دسته تقسیم کرد:
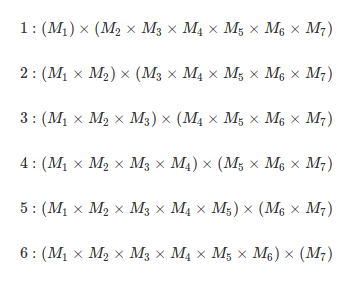
هر کدام از حاصلضربهای داخل پرانتزها، زیرمسئلهای با n < 7 هستند. همانطور که میدانید در ضرب دو ماتریس، تعداد ستونهای ماتریس اول با تعداد سطرهای ماتریس دوم برابر است. در نتیجه ابعاد هفت ماتریس فوق را به صورت زیر میتوان خلاصه کرد:
\[d_0, d_1, d_2, d_3, d_4,, d_5,, d_6, d_7 \]
که ماتریس اول $ d_0 $ سطر و $ d_1 $ ستون، ماتریس دوم $ d_1 $ سطر و $ d_2 $ ستون ... و ماتریس هفتم $ d_6 $ سطر و $ d_7 $ ستون دارد. حال تابع Mult را به گونهای تعریف میکنیم که حداقل ضربهای مورد نیاز برای ضرب ماتریسهای iام تا jام را محاسبه کند. در این صورت برای شش حالت فوق داریم:
\[1: (M_1) \times (M_2 \times M_3 \times M_4 \times M_5 \times M_6 \times M_7) : min_1 = Mult(1, 1) + Mult(2, 7) + d_0 d_1 d_7 \]
\[2: (M_1 \times M_2) \times (M_3 \times M_4 \times M_5 \times M_6 \times M_7) : min_2 = Mult(1, 2) + Mult(3, 7) + d_0 d_2 d_7 \]
\[3: (M_1 \times M_2 \times M_3)\times (M_4 \times M_5 \times M_6 \times M_7) : min_3 = Mult(1, 3) + Mult(4, 7) + d_0 d_3 d_7 \]
\[4: (M_1 \times M_2 \times M_3 \times M_4) \times ( M_5 \times M_6 \times M_7) : min_4 = Mult(1, 4) + Mult(5, 7) + d_0 d_4 d_7 \]
\[5: (M_1 \times M_2 \times M_3 \times M_4 \times M_5 ) \times (M_6 \times M_7) : min_5 = Mult(1, 5) + Mult(6, 7) + d_0 d_5 d_7 \]
\[6: (M_1 \times M_2 \times M_3 \times M_4 \times M_5 \times M_6) \times (M_7) : min_6 = Mult(1, 6) + Mult(7, 7) + d_0 d_6 d_7 \]
قسمت اول عبارتهای فوق مربوط به محاسبه زیرمسئله سمت چپ، قسمت دوم برای محاسبه زیرمسئله سمت راست و قسمت سوم ضرب دو ماتریس حاصل از زیرمسئلهها در یکدیگر است. به عنوان نمونه، در سطر سوم پس از تفکیک مسئله به دو زیرمسئله، دو ماتریس با ابعاد ($ d_0, d_3 $) و ($ d_3, d_7 $) به دست میآیند که باید در پایان کار در هم ضرب شوند. حال با مینیمم گرفتن از minkها مسئله اصلی حل میشود:
\[Mult(1, 7) = min \{ min_k \} = min \{ Mult(1, k) + Mult(k + 1, 7) + d_0 d_k d_7 \} \; \;, \qquad k = 1, \cdots, 6 \]
این رابطه را میتوان به صورت کلی برای هر شروع و انتهایی نوشت:
\[Mult(i, j) = min \{ min_k \} = min \{ Mult(i, k) + Mult(k + 1, j) + d_{i - 1} d_k d_j \} \; \;, \qquad k = i, \cdots, j - 1 \]
توجه داشته باشید که اگر i < j نباشد منطق حکم میکند که $ Mult(i, j) $ صفر شود.
با توجه به توضیحات فوق، بدنه تابع Mult در حالت کلی به این صورت خواهد بود:
int Mult(int i, int j){
int min;
min = minimum of { Mult(i, k) + Mult(k + 1, j) + d[i - 1] * d[k] * d[j] } for k = i, i + 1, i + 2, . . . , j - 1;
return min;
}
در این تابع ابعاد ماتریسها در فرم آرایه d به صورت عمومی تعریف شدهاند. ثابت شده است مرتبه اجرای چنین تابعی $ O(3^n)$ است. به نظر میرسد که این روش کارا نیست. علت آن هم وجود همپوشانی است که در ادامه به آن میپردازیم.
[برگرد بالا]
همانگونه که عنوان شد، در ضرب دو ماتریس $ M_{R \times L} $ و $ N_{L \times C} $ تعداد $ R \times L \times C $ عمل ضرب انجام میشود و حاصل ماتریسی با ابعاد $ R \times C $ است. پس اگر این حاصلضرب در ماتریس جدیدی ضرب شود، مقدار L نقشی نخواهد داشت. از این تحلیل این ایده مطرح میگردد که در ضرب زنجیرهای ماتریسها ابتدا بهتر است ابعاد بزرگ را از زنجیره حذف کنیم. به عنوان مثال در ضرب $ A_{ 1 \times 3} \times B_{3 \times 2} \times C_{2 \times 5 } $ ابتدا ضرب $ D_{ 1 \times 2 } = A_{ 1 \times 3} \times B_{3 \times 2} $ انجام شده و سپس $ D_{ 1 \times 2 } \times C_{2 \times 5 } $ محاسبه شود. این ترتیب ضرب نسبت به ترتیب $ A_{ 1 \times 3} \times (B_{3 \times 2} \times C_{2 \times 5 }) $ عملیات ضرب کمتری دارد. چنین الگوریتمی همواره به پاسخ درست منتهی نمیشود. در مثال ابتدای نوشته مشخص شد که محاسبه $ (A_{3 \times 7} \times B_{7 \times 8 }) \times C_{8 \times 4} $ تعداد ضرب کمتری نسبت به $ A_{3 \times 7} \times (B_{7 \times 8 } \times C_{8 \times 4}) $ نیاز دارد؛ اما بر اساس ایده مطرح شده ترتیب $ A_{3 \times 7} \times (B_{7 \times 8 } \times C_{8 \times 4}) $ برای ضرب انتخاب میشود.
[برگرد بالا]
حال به سراغ برنامهنویسی پویا رفته و دو شرط لازم این روش برای حل مسائل بهینهسازی را بررسی میکنیم:
1- همپوشانی: برای بررسی وجود همپوشانی در تابع فوق دو روش وجود دارد. اول اینکه درخت فراخوانیهای بازگشتی تابع را به ازای یک n کوچک رسم کرده و فراخوانیهای تکراری را مشاهده کنید. دومین روش این است که به مرتبه تعداد فراخوانیها توجه کنید. با توجه به اینکه مقادیر i و j اعداد طبیعی کوچکتر از n هستند، تعداد کل حالتهای فراخوانی تابع Mult با پارامترهای مختلف از مرتبه $O(n^2)$ خواهد بود. در حالی که ثابت شده است تعداد کل فراخوانیهای تابع از مرتبه $ O(3^n)$ است. این اختلاف تنها میتواند ناشی از فراخوانیهای تکراری باشد.
2- اصل بهینگی: اگر بنا باشد پرانتزبندی کل عبارت بهینه شود، پرانتزبندی زیرمسئلهها هم باید بهینه باشند. یعنی بهینه بودن مسئله، بهینه بودن زیرمسئلهها را ایجاب میکند.
پس میتوان از روش برنامهنویسی پویا استفاده کرد.
در روش برنامهنویسی پویا اغلب از یک آرایه برای ذخیره نتایج جهت استفاده مجدد استفاده شده و زیرمسائل به صورت جزء به کل حل میشوند. در مورد این مسئله، ابتدا زیرمسائلی که تنها از دو ماتریس تشکیل شدهاند محاسبه میشوند. سپس زیرمسائلی که از سه ماتریس تشکیل شدهاند محاسبه میشوند. این دسته از زیرمسائل به زیرمسائلی متشکل از دو ماتریس تجزیه میشوند که قبلا محاسبات آنها صورت گرفته و نتایج آنها در آرایه ذخیره شدهاند. در نتیجه نیاز به محاسبه مجدد آنها نیست. به همین ترتیب در مرحله بعد زیرمسائل با چهار ماتریس محاسبه میشوند و الی آخر.
برای پیادهسازی این روش، آرایه دو بعدی M را منطبق با عملکرد تابع Mult تعریف میکنیم:
M[i][j] = Min { M[i][k] + M[k + 1][j] + d[ i] * d[k + 1] * d [j] }
i ≤ k ≤ j - 1, 0 < i < j < n + 1, M[i][i] = 0
توجه داشته باشید که اندیس شروع آرایهها را یک در نظر گرفتهایم و تنها از قسمت بالای قطر اصلی ماتریس استفاده میکنیم. تابع زیر محاسبات لازم را جهت ساخت این ماتریس انجام میدهد:
int Mult(int n){
int i, j;
for(i = 1 ; i <= n ; i++)
M[i][i] = 0;
for(i = 1 ; i < n ; i++)
for(j = 1 ; j <= n - i ; j++)
M[j][i + j] = Minimum of { M[i][k] + M[k + 1][j] + d[i - 1] * d[k] * d[j] } for k = i, i + 1, i + 2, ..., j - 1
return M[1][n];
}
تابع مقدار [M[1][n را باز میگرداند که همان تعداد ضربهای لازم جهت محاسبه ضرب زنجیرهای n ماتریس در حالت پرانتزبندی بهینه است. این تابع دو حلقه تکرار دارد که مرتبه $ O(n^2)$ را نشان میدهند. اما یافتن مینیمم دادهها درون حلقه داخلی نیز وجود دارد که از مرتبه $O(n)$ است. در نتیجه مرتبه کل تابع فوق $O(n^3)$ خواهد بود که در مقایسه با $O(3^n)$ بهبود چشمگیری را نشان میدهد.
مزیت دیگر این روش - که از اصل بهینگی ناشی میشود - این است که با انجام این محاسبات، نه تنها مسئله اصلی که حالت بهینه همه زیرمسائل حل شده است. به عنوان نمونه، [M[2][4 تعداد ضربهای لازم در پرانتزبندی بهینه ماتریسهای دوم تا چهارم را نشان میدهد.
در پایان باید توجه داشته باشید که:
1- در دو تابعی که اینجا آورده شده است، تنها تعداد ضربهای لازم در پرانتزبندی بهینه محاسبه گشته و شیوه پرانتزبندی مد نظر نیست.
2- به نظر میرسد روش برنامهنویسی پویا از روش تقسیم و حل قدرتمندتر است! اما همیشه اینگونه نیست. ما در همه حال باید به دو شرط اساسی امکان استفاده از برنامهنویسی پویا جهت طراحی الگوریتم توجه داشته باشیم. در بسیاری از مسائل این دو شرط برقرار نیستند و ممکن است طراحی الگوریتم حل آنها با استفاده از روش تقسیم و حل کاراتر باشد.