دترمینان ماتریس مربعی - که به صورت $ \vert A \vert $ یا $ det( A ) $ نمایش داده میشود - یکی از مفاهیم مشهور جبر خطی است که کاربردهای بسیاری در علوم مختلف دارد. امکان محاسبه سریع دترمینان یک ماتریس با ابعاد بزرگ بحث مهمی است که در ادامه سه روش محاسباتی رایج و پیچیدگی زمانی آنها مرور خواهند شد.
[برگرد بالا]
طبق تعریف دترمینان اگر اندازه ابعاد ماتریس مربعی یک باشد ($n = 1$)، دترمینان همان مقدار تکعضو آن است. یعنی:
\[ det( \begin{bmatrix} a \end{bmatrix} ) = \vert \begin{bmatrix} a \end{bmatrix} \vert = a \]
اما اگر مرتبه ماتریس بزرگتر از یک باشد ($n > 1$) دترمینان را به یکی از روشهای زیر میتوان محاسبه کرد.

[برگرد بالا]
بسط لاپلاس (یا بسط همسازهای) برای محاسبه دترمینان ماتریس مرتبه $n$، به فرم زیر است:
\[ \vert A \vert = \sum_{j=1}^{n} {(-1)}^{i+j} a_{ij} \vert A_{ij} \vert \qquad , \qquad 1 \leq i \leq n \]
یا
\[ \vert A \vert = \sum_{i=1}^{n} {(-1)}^{i+j} a_{ij} \vert A_{ij} \vert \qquad , \qquad 1 \leq j \leq n \]
که در حالت اول بسط بر اساس سطر دلخواه $i$ و در حالت دوم بر اساس ستون دلخواه $j$ صورت گرفته است. منظور از $A_{ij}$ (ماتریس کهاد) ماتریسی است که از حذف سطر $i$ام و ستون $j$ام ماتریس اصلی به دست آمده است.
به عنوان مثال اگر ماتریس مربعی $A$ به صورت زیر تعریف شده باشد:
\[ A = \begin{bmatrix} 1 & -1 & 8 \\ 0 & 3 & 1 \\ 2 & 2 & 1 \end{bmatrix} \]
دترمینان آن با بسط روی سطر اول به این ترتیب محاسبه میشود:
\[ \begin{vmatrix} 1 & -1 & 8 \\ 0 & 3 & 1 \\ 2 & 2 & 1 \end{vmatrix} = {(-1)}^{1+1} \times 1 \times \begin{vmatrix} 3 & 1 \\ 2 & 1 \end{vmatrix} + {(-1)}^{1+2} \times (-1) \times \begin{vmatrix} 0 & 1 \\ 2 & 1 \end{vmatrix} \] \[ + {(-1)}^{1+3} \times 8 \times \begin{vmatrix} 0 & 3 \\ 2 & 2 \end{vmatrix} = 1 \times \Big({(-1)}^{1+1} \times 3 \times \vert 1 \vert + {(-1)}^{1+2} \times 1 \times \vert 2 \vert \Big) \] \[ + 1 \times \Big({(-1)}^{1+1} \times 0 \times \vert 1 \vert + {(-1)}^{1+2} \times 1 \times \vert 2 \vert \Big) \] \[ + 8 \times \Big({(-1)}^{1+1} \times 0 \times \vert 2 \vert + {(-1)}^{1+2} \times 3 \times \vert 2 \vert \Big) \] \[ = 1 \times( 3 - 2 ) + 1 \times ( 0 - 2 ) + 8 \times ( 0 - 6 ) = 1 - 2 - 48 = -49 \]
و با بسط روی ستون دوم:
\[ \begin{vmatrix} 1 & -1 & 8 \\ 0 & 3 & 1 \\ 2 & 2 & 1 \end{vmatrix} = {(-1)}^{1+2} \times (-1) \times \begin{vmatrix} 0 & 1 \\ 2 & 1 \end{vmatrix} + {(-1)}^{2+2} \times 3 \times \begin{vmatrix} 1 & 8 \\ 2 & 1 \end{vmatrix} \] \[ + {(-1)}^{3+2} \times 2 \times \begin{vmatrix} 1 & 8 \\ 0 & 1 \end{vmatrix} = 1 \times \Big( {(-1)}^{1+2} \times 1 \times \vert 2 \vert + {(-1)}^{2+2} \times 1 \times \vert 0 \vert \Big) \] \[ + 3 \times \Big( {(-1)}^{1+2} \times 8 \times \vert 2 \vert + {(-1)}^{2+2} \times 1 \times \vert 1 \vert \Big) \] \[ - 2 \times \Big( {(-1)}^{1+2} \times 8 \times \vert 0 \vert + {(-1)}^{2+2} \times 1 \times \vert 1 \vert \Big) \] \[ = 1 \times( -2 + 0 ) + 3 \times ( -16 + 1 ) - 2 \times ( 0 + 1 ) = -2 - 45 -2 = -49 \]
توجه داشته باشید که منظور از $\vert \; \vert $ علامت قدرمطلق نیست.
انتخاب سطر یا ستون مناسب برای محاسبه دترمینان با استفاده از این روش وابسته به مقادیر درایههای آن است. به عنوان مثال اگر تعداد درایههای صفر یک سطر یا یک ستون زیاد باشد، بهتر است از آن سطر یا ستون برای بسط استفاده کنیم. مثلا در ماتریس زیر، بهتر است از ستون اول برای بسط استفاده کنیم:
\[ \begin{vmatrix} 1 & -1 & 8 \\ 0 & 3 & 1 \\ 0 & 2 & 1 \end{vmatrix} = {(-1)}^{1+1} \times 1 \times \begin{vmatrix} 3 & 1 \\ 2 & 1 \end{vmatrix} + {(-1)}^{2+1} \times 0 \times \begin{vmatrix} -1 & 8 \\ 2 & 1 \end{vmatrix} \] \[ + {(-1)}^{3+1} \times 0 \times \begin{vmatrix} -1 & 8 \\ 3 & 1 \end{vmatrix} = 1 \times \Big( {(-1)}^{1+1} \times 3 \times \vert 1 \vert + {(-1)}^{2 + 1} \times 2 \times \vert 1 \vert \Big) + 0 + 0 = 1 \]
[برگرد بالا]
همانطور که از تعریف مشخص است، در روش بسط لاپلاس، محاسبه دترمینان یک ماتریس مرتبه $n$، به محاسبه دترمینان $n$ ماتریس کهاد از مرتبه $n - 1$ شکسته میشود. اگر عمل اصلی محاسبات را اعمال ضرب و جمع در نظر گرفته و $T_1(n)$ تعداد این اعمال را برای محاسبه دترمینان ماتریس مرتبه $n$ به روش بسط لاپلاس نشان دهد، میتوان نوشت:
\[ T_1( n ) = n T_1( n - 1 ) + n + n + n - 1 = n T_1( n - 1 ) + 3n - 1 \qquad, \qquad T_1( 1 ) = 0 \]
$ n T_1( n - 1) $: تعداد اعمال لازم برای محاسبه زیرمسائل
$n$: تعداد ضربهای بین $ a_{ij} $ و توانهای زوج یا فرد منفی یک
$n$: تعداد ضربهای بین $ a_{ij} $ و $ det( A_{ij})$
$n - 1$: تعداد جمعهای لازم برای محاسبه نهایی
حل این رابطه بازگشتی نشان میدهد $T_1(n)$ از مرتبه $O( n! ) $ است که برای $n$های بزرگ کارایی ندارد.
[برگرد بالا]
برای محاسبه دترمینان یک ماتریس مربعی، خواصی وجود دارد که به اعمال مقدماتی سطری و ستونی مشهور بوده و عموما از روش بسط لاپلاس ثابت میشوند. تعدادی از این خواص به شرح زیر هستند:
1- جابجا کردن دو سطر (یا دو ستون) ماتریس، مقدار دترمینان را قرینه میکند. در مثال زیر جای سطر اول و دوم عوض شده است:
\[ \begin{vmatrix} 1 & -1 & 8 \\ 3 & 3 & 1 \\ 7 & 2 & 1 \end{vmatrix} = - \begin{vmatrix} 3 & 3 & 1 \\ 1 & -1 & 8 \\ 7 & 2 & 1 \end{vmatrix} \]
2- اگر تمام درایههای یک سطر (یا یک ستون) ماتریس در عددی مانند k ضرب شود، حاصل دترمینان نیز k برابر میشود. در مثال زیر سه برابر بودن درایههای متناظر سطر دوم ماتریس سمت چپ، نسبت به سطر دوم ماتریس سمت راست، مقدار دترمینان آن را نیز سه برابر کرده است:
\[ \begin{vmatrix} 1 & -1 & 8 \\ 3 & 3 & 6 \\ 7 & 2 & 1 \end{vmatrix} = 3 \times \begin{vmatrix} 1 & -1 & 8 \\ 1 & 1 & 2 \\ 7 & 2 & 1 \end{vmatrix} \]
3- اگر ضریب ثابتی از درایههای یک سطر (یا یک ستون) ماتریس به سطر (یا ستون) دیگری اضافه شود، مقدار دترمینان تغییر نمیکند. در مثال زیر پنج برابر سطر اول به سطر سوم اضافه شده است:
\[ \begin{vmatrix} 1 & -1 & 8 \\ 3 & 3 & 6 \\ 7 & 2 & 1 \end{vmatrix} = \begin{vmatrix} 1 & -1 & 8 \\ 3 & 3 & 6 \\ 7 + 5 \times 1 & 2 + 5 \times (-1) & 1 + 5 \times 8 \end{vmatrix} \]
4- دترمینان یک ماتریس مثلثی (ماتریسی که تمامی درایههای بالای قطر اصلی یا پایین قطر اصلی و یا هر دو صفر باشند) برابر حاصلضرب درایههای قطر اصلی آن است:
\[ \begin{vmatrix} 1 & -1 & 8 \\ 0 & 3 & 6 \\ 0 & 0 & 4 \end{vmatrix} = 1 \times 3 \times 4 = 12 \]
5- ماتریسی که تمامی درایههای یک سطر (یا یک ستون) آن صفر باشد، دترمینان آن نیز صفر خواهد بود:
\[ \begin{vmatrix} 1 & -1 & 8 \\ 9 & 3 & 6 \\ 0 & 0 & 0 \end{vmatrix} = 0 \]
در روش گاوس مراحل زیر انجام میشود:
مرحله اول: اگر درایه سطر اول و ستون اول صفر است، سطری را که مقدار درایه ستون اول آن صفر نباشد به سطر اول منتقل میکنیم. این عمل مقدار دترمینان را تغییر علامت میدهد. اگر چنین سطری یافت نشد، یعنی تمامی درایههای ستون اول صفر هستند. پس بنا به خاصیت شماره پنج، مقدار دترمینان صفر شده و انجام مراحل بعدی نیاز نیست.
مرحله دوم: ضریب مناسبی از مقدار درایه سطر اول و ستون اول را که درایه ستون اول هر سطر را صفر کند، به هر سطر به صورت مجزا اضافه میکنیم. اگر مقدار درایه ستون اول آن ستون، از قبل صفر باشد، نیاز به انجام عمل خاصی نیست. این عمل مقدار دترمینان را تغییر نمیدهد.
در مثال زیر، ستون اول سطر دوم مقدار صفر دارد. پس نیاز به انجام عملیات خاصی نیست. اما مقدار درایه ستون اول سطر سوم غیرصفر است. پس با اضافه کردن ضریب مناسبی از درایههای سطر اول به این سطر، مقدار آن را نیز صفر میکنیم. مقدار این ضریب با توجه به مقدار درایه سطر اول و ستون اول مشخص میشود که در این مثال منفی دو است:
\[ \begin{vmatrix} 1 & -1 & 8 \\ 0 & 3 & 1 \\ 2 & 1 & 1 \end{vmatrix} = \begin{vmatrix} 1 & -1 & 8 \\ 0 & 3 & 1 \\ 2 + (-2) \times 1 & 1 + (-2) \times (-1) & 1 + (-2) \times 8 \end{vmatrix} = \begin{vmatrix} 1 & -1 & 8 \\ 0 & 3 & 1 \\ 0 & 3 & -15 \end{vmatrix} \]
مرحله سوم: در ماتریس به دست آمده، ستون اول آن، به غیر از سطر اول همه صفر هستد. بسط لاپلاس دترمینان ماتریس را بر اساس ستون اول انجام میدهیم:
\[ \begin{vmatrix} 1 & -1 & 8 \\ 0 & 3 & 1 \\ 0 & 3 & -15 \end{vmatrix} = {(-1)}^{1+1} \times 1 \times \begin{vmatrix} 3 & 1 \\ 3 & -15 \end{vmatrix} = \begin{vmatrix} 3 & 1 \\ 3 & -15 \end{vmatrix} \]
مرحله چهارم: محاسبه دترمینان ماتریس از مرتبه n به محاسبه دترمینان ماتریس مرتبه n - 1 تقلیل یافته است. با ادامه این مراحل برای این ماتریس، تا رسیدن به ماتریسی از مرتبه یک، مقدار دترمینان اصلی محاسبه میشود:
\[ \begin{vmatrix} 3 & 1 \\ 3 & -15 \end{vmatrix} = \begin{vmatrix} 3 & 1 \\ 3 + (-1) \times 3 & -15 + (-1) \times 1 \end{vmatrix} = \Big( (-1) ^ {1+1} \times 3 \times \vert -16 \vert \Big) = -48 \]
و در نتیجه:
\[ \begin{vmatrix} 1 & -1 & 8 \\ 0 & 3 & 1 \\ 2 & 1 & 1 \end{vmatrix} = -48 \]
[برگرد بالا]
اعمال ضرب و جمع را اعمال اصلی این روش در نظر گرفته و $ T_2( n ) $ را تعداد این اعمال برای محاسبه دترمینان به روش گاوس تعریف میکنیم. برای صفر کردن ستون اول هر سطر، ضریب مشخصی را محاسبه می کنیم که به یک عمل تقسیم (همارز ضرب) نیاز دارد. سپس حاصلضرب این ضریب در درایههای سطر اول را به درایههای متناظر آن سطر اضافه میکنیم. در نتیجه این مرحله برای هر سطر n عمل ضرب و $n$ عمل جمع دارد که برای $n - 1$ سطر باید اعمال شود. در پایان نیز با بسط لاپلاس روی ستون اول و یک عمل ضرب، به محاسبه دترمینان مرتبه $n - 1$ میرسیم. پس میتوان نوشت:
\[ T_2(n) = 1 + (n-1)(n+n) + T_2( n-1) + 1 = T_2 ( n-1) + 2n^2 - 2n + 2 \; \; , \; \; T_2(1) = 0 \]
چنین رابطه بازگشتیای از مرتبه $ O( n^ 3 ) $ است که بهبود چشمگیری در مقایسه با روش بسط لاپلاس با مرتبه $ O(n!) $ دارد.
در واقع هدف از این الگوریتم، تبدیل ماتریس به یک ماتریس بالامثلثی (یا پایینمثلثی)، با استفاده از عملیات مقدماتی سطری و ستونی است. طبق خاصیت چهارم، مقدار دترمینان چنین ماتریسی برابر حاصلضرب درایههای قطر اصلی آن است:
\[ \begin{vmatrix} 1 & -1 & 8 \\ 0 & 3 & 1 \\ 2 & 1 & 1 \end{vmatrix} = \begin{vmatrix} 1 & -1 & 8 \\ 0 & 3 & 1 \\ 0 & 3 & -15 \end{vmatrix} = \begin{vmatrix} 1 & -1 & 8 \\ 0 & 3 & 1 \\ 0 & 0 & -16 \end{vmatrix} = 1 \times 3 \times -16 = -48 \]
پیادهسازی این الگوریتم به سه حلقه تکرار تو در تو نیاز دارد که با یک حساب سرانگشتی مرتبه $O(n^3)$ را نشان میدهد.
توجه: در برخی منابع این روش با عنوان گاوس-جردن معرفی میشود.
[برگرد بالا]
در بخش ضمیمه کتاب «حساب دیفرانسیل و انتگرال و هندسه تحلیلی» نوشته «جرج بی. توماس» و «راس ال. فینی»، فرمول تحویل از مقاله میلر به صورت زیر بیان شده است:
\[ \vert A \vert = \Big( \frac{1}{a_{11}} \Big)^{n-2} \begin{vmatrix} \begin{vmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{vmatrix} & \begin{vmatrix} a_{11} & a_{13} \\ a_{21} & a_{23} \end{vmatrix} & \cdots & \begin{vmatrix} a_{11} & a_{1n} \\ a_{21} & a_{2n} \end{vmatrix} \\ \begin{vmatrix} a_{11} & a_{12} \\ a_{31} & a_{32} \end{vmatrix} & \begin{vmatrix} a_{11} & a_{13} \\ a_{31} & a_{33} \end{vmatrix} & \cdots & \begin{vmatrix} a_{11} & a_{1n} \\ a_{31} & a_{3n} \end{vmatrix} \\ \vdots & \vdots & \ddots & \vdots \\ \begin{vmatrix} a_{11} & a_{12} \\ a_{n1} & a_{n2} \end{vmatrix} & \begin{vmatrix} a_{11} & a_{13} \\ a_{n1} & a_{n3} \end{vmatrix} & \cdots & \begin{vmatrix} a_{11} & a_{1n} \\ a_{n1} & a_{nn} \end{vmatrix} \end{vmatrix} \]
یا به عبارت دیگر:
\[ \vert A \vert = \Big( \frac{1}{a_{11}} \Big)^{n-2} \begin{vmatrix} c_{11} & c_{12} & \cdots & c_{1(n-1)} \\ c_{21} & c_{22} & \cdots & c_{2(n-1)} \\ \vdots & \vdots & \ddots & \vdots \\ c_{(n-1)1} & c_{(n-1)2} & \cdots & c_{(n-1)(n-1)} \end{vmatrix} \; , \; c_{ij} = \begin{vmatrix} a_{11} & a_{i(j+1)} \\ a_{(i+1)1} & a_{(i+1)(j+1)} \end{vmatrix} \]
به عنوان مثال:
\[ \begin{vmatrix} 2 & 4 & 1 & 1 \\ 0 & 2 & 1 & -1 \\ -2 & 1 & 2 & 0 \\ -1 & 1 & 0 & 3 \end{vmatrix} = \Big( \frac{1}{2} \Big)^{4-2} \begin{vmatrix} \begin{vmatrix} 2 & 4 \\ 0 & 2 \end{vmatrix} & \begin{vmatrix} 2 & 1 \\ 0 & 1 \end{vmatrix} & \begin{vmatrix} 2 & 1 \\ 0 & -1 \end{vmatrix} \\ \begin{vmatrix} 2 & 4 \\ -2 & 1 \end{vmatrix} & \begin{vmatrix} 2 & 1 \\ -2 & 2 \end{vmatrix} & \begin{vmatrix} 2 & 1 \\ -2 & 0 \end{vmatrix} \\ \begin{vmatrix} 2 & 4 \\ -1 & 1 \end{vmatrix} & \begin{vmatrix} 2 & 1 \\ -1 & 0 \end{vmatrix} & \begin{vmatrix} 2 & 1 \\ -1 & 3 \end{vmatrix} \end{vmatrix} \] \[ = \Big( \frac{1}{2} \Big)^{2} \begin{vmatrix} 4 & 2 & -2 \\ 10 & 6 & 2 \\ 6 & 1 & 7 \end{vmatrix} = \Big( \frac{1}{2} \Big)^{2} \Big( \frac{1}{4} \Big)^{3-2} \begin{vmatrix} 4 & 28 \\ -8 & 40 \end{vmatrix} = \frac{1}{4} \times \frac{1}{4} \times (160+224) = 24 \]
واضح است که برای چنین محاسبهای باید $a_{11}$ غیر صفر باشد. اگر اینچنین نبود، طبق اعمال مقدماتی سطر و ستون باید با جابجایی سطرها مقدار آن را غیر صفر کرد.
این فرمول، مسئله از مرتبه $n$ را به یک زیرمسئله از مرتبه $n - 1$، و $ {( n - 1 )}^2 $ زیرمسئله از مرتبه 2 تبدیل میکند.
[برگرد بالا]
اگر $ T_3( n ) $ تعداد اعمال ضرب و جمع برای محاسبه به این روش باشد، میتوان نوشت:
\[ T_3(n)=n-1+ T_3(n-1)+(n-1)^2 T_3(2) = T_3(n-1)+3n^2-5n+2 \;, \; T_3(2) = 3 \]
$n - 1$: تعداد تقسیم و ضربهای (یک تقسیم و $n - 2$ ضرب) لازم برای محاسبه توان $(n- 2)$ام معکوس $ a_{11} $ و ضرب آن در دترمینان
$T_3( n - 1 ) $: تعداد اعمال لازم برای حل زیرمسئله
${( n - 1 )}^2 T_3( 2 )$: تعداد اعمال لازم برای محاسبه درایههای ماتریس زیرمسئله
حل این رابطه بازگشتی نیز مرتبه پیچیدگی $ O(n^3) $ را نشان میدهد.
[برگرد بالا]
عملکرد سه روش بررسی شده را میتوان اینگونه خلاصه کرد که:
1- محاسبه پیچیدگی زمانی روشهای سهگانه فوق نشان میدهد، کارآیی زمانی دو روش گاوس و فرمول تحویل تقریبا یکسان بوده و بسیار بهتر از روش بسط لاپلاس هستند.
2- فضای مصرفی هر سه روش در صورت پیادهسازی بهینه آنها، همان فضای لازم برای ذخیره یک ماتریس مربعی از مرتبه $n$ است.
3- هر سه روش ظاهری بازگشتی - با روش تقسیم و غلبه - دارند که حل مسئله از مرتبه $n$ را به حل زیرمسئله یا زیرمسائلی از مرتبه $n - 1$ تقسیم میکنند. اما پیادهسازی غیربازگشتی این روشها نیز ممکن است که در روش گاوس توضیح مختصری داده شد.
4- بر اساس روش بسط لاپلاس و با استفاده از استقرای ریاضی، میتوان ثابت کرد که اگر تمامی درایههای یک ماتریس مربعی اعداد صحیح باشند، دترمینان آن نیز عدد صحیح خواهد بود. روش بسط لاپلاس صحیح بودن عدد دترمینان را در این شرایط تضمین میکند. چرا که تنها از اعمال جمع و ضرب تشکیل شده است که صحیح بودن عدد را تغییر نمیدهند. اما دو روش دیگر - با توجه به این که شامل عمل تقسیم نیز هستند - در زمان پیادهسازی ممکن است خطای محاسباتی ایجاد کنند. چرا که اکثر زبانهای برنامهنویسی اعداد را به دو فرم صحیح یا اعشاری - با دقت مشخص - ذخیره میکنند. بنابراین اعداد گویای غیرصحیح به صورت تقریبی ذخیره شده و در محاسبات هم به همان صورت تقریبی به کار میروند.
دترمینان ماتریس $A$ را که توسط بسط لاپلاس محاسبه کردیم، با استفاده از روش گاوس و با فرض ذخیره اعداد گویا به صورت اعشاری - با دقت شش رقم - مجددا محاسبه میکنیم:
\[ \begin{vmatrix} 1 & -1 & 8 \\ 0 & 3 & 1 \\ 2 & 2 & 1 \end{vmatrix} = \begin{vmatrix} 1 & -1 & 8 \\ 0 & 3 & 1 \\ 2 + (-2) \times 1 & 2 + (-2) \times (-1) & 1 + (-2) \times 8 \end{vmatrix} = \] \[ \begin{vmatrix} 1 & -1 & 8 \\ 0 & 3 & 1 \\ 0 & 4 & -15 \end{vmatrix} = \begin{vmatrix} 1 & -1 & 8 \\ 0 & 3 & 1 \\ 0 & 4 + (-1.333333) \times 3 & -15 + (-1.333333) \times 1 \end{vmatrix} \] \[ = \begin{vmatrix} 1 & -1 & 8 \\ 0 & 3 & 1 \\ 0 & 0 & -16.333333 \end{vmatrix} = -48.999999 \]
این مسئله زمانی اهمیت دارد که محاسبه دقیق مد نظر بوده و امکان انجام عملیات حسابی روی اعداد گویا وجود نداشته باشد.
[برگرد بالا]
دترمینان ماتریس سه در سه با استفاده از بسط لاپلاس به این ترتیب محاسبه میشود:
\[ \begin{vmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{vmatrix} \] \[ = (-1)^{1+1}a_{11} \begin{vmatrix} a_{22} & a_{23} \\ a_{32} & a_{33} \end{vmatrix} + (-1)^{1+2}a_{12} \begin{vmatrix} a_{21} & a_{23} \\ a_{31} & a_{33} \end{vmatrix} + (-1)^{1+3}a_{13} \begin{vmatrix} a_{21} & a_{22} \\ a_{31} & a_{32} \end{vmatrix} \] \[ = a_{11} (a_{22} a_{33}-a_{23}a_{32} ) - a_{12} (a_{21} a_{33}-a_{23}a_{31} ) + a_{13} (a_{21} a_{32}-a_{22}a_{31} ) \] \[ = a_{11} a_{22} a_{33} + a_{12} a_{23} a_{31} + a_{13} a_{21} a_{32} - a_{11} a_{23} a_{32} - a_{12} a_{21} a_{33} - a_{13} a_{22} a_{31} \]
این عملیات را میتوان با کمک گرفتن از یک تصویر ذهنی به ترتیب زیر انجام داد:
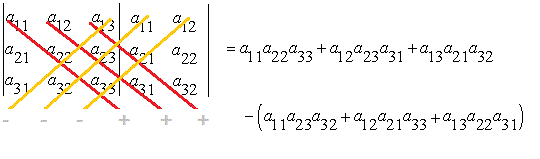
زمانی که در یک برنامه نیاز به محاسبه دترمینان ماتریس 3 در 3 باشد، پیادهسازی کد با این روش به صرفهتر از پیادهسازی با روشهای بحث شده قبلی است.
تذکر: روش ساروس صرفا برای محاسبه دترمینان ماتریسهای سه در سه بوده و در سایر ابعاد قابل استفاده نیست.