دنباله اعداد کاتالان (Catalan Numbers) یکی از دنباله‌های عددی مشهور ریاضیات است که برای عدد نامنفی n به صورت $C_n$ نمایش داده می‌شود.
$C_n:\qquad 1,\;1,\;2,\;5,\;14,\;42,\;132,\;429,\;1430,\;4862,\;16796,\;\cdots$
این دنباله کاربردهای بسیاری در مسائل شمارشی دارد. از جمله:
1- تعداد درخت‌های دودویی با n رأس داخلی برابر $C_n$ است:
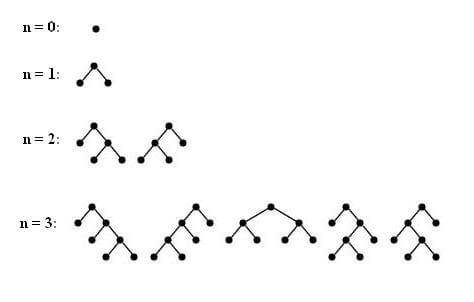
2- تعداد درخت‌ها با n یال برابر $C_n$ است:
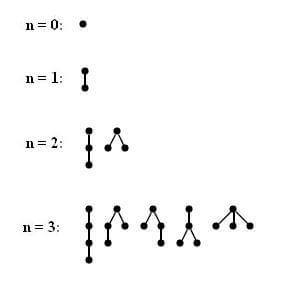
3- تعداد پرانتزبندی‌های صحیح با استفاده از n جفت پرانتز باز و بسته برابر $C_n$ است:
n = 1: ()
n = 2: (()) , () ()
n = 3: ((())) , (()) () , () (()) , (() ()) , () () ()
4- تعداد پرانتزبندی‌های صحیح n عبارت ریاضی برابر $C_{n-1}$ است:
n = 1: (A)
n = 2: (A B)
n = 3: ((A B) C) , (A (B C))
n = 4: (((A B) C) D) , ((A (B C)) D) , ((A B) (C D)) , (A ((B C) D) , (A (B (C D)))
5- تعداد روش‌های مثلث‌بندی یک چندضلعی محدب با n + 2 ضلع برابر $C_n$ است:
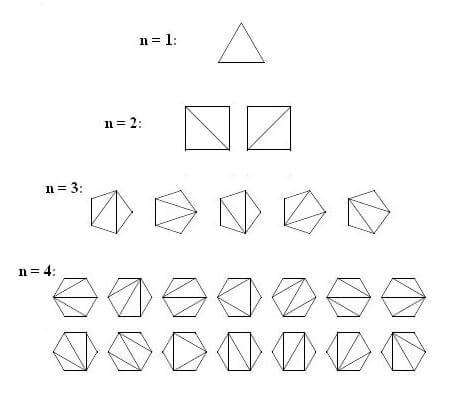
6- ...
با بررسی تحلیلی این مسائل، رابطه بازگشتی زیر برای محاسبه جملات دنباله اعداد کاتالان به دست آمده است:
\[ C_n = \sum_{i=0}^{n-1} \; C_i \; C_{n-i-1} \qquad , \qquad C_0 = 1 \]
این تعریف، مقدار جمله nام دنباله را به مقادیر تمام جملات قبلی وابسته می‌کند. به عنوان مثال:
$C_1 = C_0 \times C_0 = 1 \times 1 = 1$
$ C_2 = C_0 \times C_1 + C_1 \times C_0 = 1 \times 1 + 1 \times 1 = 2 $
$ C_3 = C_0 \times C_2 + C_1 \times C_1 + C_2 \times C_0 = 1 \times 2 + 1 \times 1 + 2 \times 1 = 5 $
پیاده‌سازی به روش تقسیم و غلبه
[برگرد بالا]
اولین و ساده‌ترین پیاده‌سازی برای محاسبه اعداد کاتالان، پیاده‌سازی بازگشتی رابطه فوق است:
long catalan_1(int n){
if(n == 0)
return 1;
long i, sum = 0;
for(i = 0 ; i < n ; i++)
sum += (catalan_1(i) * catalan_1(n - i - 1));
return sum;
}
این قطعه کد یک پیاده‌سازی تقسیم و غلبه برای محاسبه است که تعداد اعمال ضرب و جمع مورد نیاز آن از مرتبه اجرای نمایی $ \theta( 3^n)$ است (چرا؟). چنین مرتبه‌ای نشان از عدم کارایی محاسبه با این روش دارد.
پیاده‌سازی به روش برنامه‌نویسی پویا
[برگرد بالا]
روش تقسیم و غلبه را کنار گذاشته و روش برنامه‌نویسی پویا را امتحان می‌کنیم. در این روش به جای حرکت از کل به جزء و محاسبه بازگشتی، از جزء به کل حرکت کرده و جملات دنباله از مقادیر کوچکتر به مقادیر بزرگتر محاسبه می‌شود:
long catalan_2(int n, long catalan[]){
int i, j;
catalan[0] = 1;
for(i = 1 ; i <= n ; i++){
catalan[i] = 0;
for(j = 0 ; j < i ; j++)
catalan[i] += catalan[j] * catalan[i - j - 1];
}
return catalan[n];
}
همانگونه که از ساختار حلقه‌های تکرار مشخص است، مرتبه اجرای این پیاده‌سازی $\theta(n^2)$ است که در مقایسه با تابع قبلی بهبود چشم‌گیری دارد. علاوه بر این، با استفاده از این تابع تمام جملات کوچکتر یا مساوی n محاسبه شده و در آرایه catalan ذخیره می‌شود.
رابطه غیربازگشتی اعداد کاتالان
[برگرد بالا]
تا به این جا با تعریف بازگشتی دنباله کاتالان سر و کار داشتیم. اما این دنباله بازگشتی را می‌توان با استفاده از روابط ریاضی حل کرده و به یک رابطه غیربازگشتی دست یافت.
حل تحلیلی دنباله کاتالان با استفاده از توابع مولد رابطه زیر را نتیجه می‌دهد:
\[ C_n=\frac{1}{n+1} \begin{pmatrix} 2n \\ n \end{pmatrix} \]
این رابطه اعداد کاتالان را مستقل از جملات قبلی محاسبه می‌کند. اما نیاز به محاسبه ترکیب دو عدد دارد:
long catalan_3(int n){
long c = combination(2 * n, n);
return (c / n + 1);
}
پیاده‌سازی تابع combination روش‌های مختلفی دارد که ترکیب $C(2n, n)$ را در بهترین حالت از مرتبه اجرای $\theta(n^2)$ محاسبه می‌کند. در نتیجه این روش مزیتی نسبت به روش برنامه‌نویسی پویا ندارد. اما بر اساس این رابطه، می‌توان رابطه بازگشتی زیر را نتیجه گرفت:
\[ C_n=\frac{2(2n-1)}{n+1}C_{n-1} \qquad , \qquad C_0=1 \]
و آنرا به صورت زیر پیاده‌سازی کرد:
long catalan_4(int n){
if(n == 0)
return 1;
return (((4 * n - 2) * catalan_4(n - 1)) / (n + 1));
}
چنین تابعی اعداد کاتالان را به صورت بازگشتی و با مرتبه اجرای $\theta(n)$ محاسبه می‌کند. این بهبود در مرتبه را می‌توان با پیاده‌سازی به روش برنامه‌نویسی پویا تعمیم داد و علاوه بر پیاده‌سازی غیربازگشتی، تمامی جملات کوچکتر یا مساوی n را ذخیره کرد:
long catalan_5(int n, long catalan[]){
int i;
catalan[0] = 1;
for(i = 1 ; i <= n ; i++)
catalan[i] = (((4 * i - 2) * catalan[i - 1]) / (i + 1));
return catalan[n];
}
به این ترتیب تمامی جملات دنباله کاتالان تا یک n دلخواه با مرتبه اجرای $\theta(n)$ محاسبه می‌شود.