ترکیب (Combination) به انتخاب تعدادی عنصر از یک مجموعه بزرگتر بدون در نظر گرفتن ترتیب آنها اشاره دارد. در ترکیب، برخلاف جایگشت (Permutation)، ترتیب انتخاب عناصر مهم نیست. این مفهوم در ریاضیات کاربرد گستردهای دارد و یکی از موارد اصلی استفاده از آن در محاسبهی ضرایب بسط دوجملهای است. ترکیبها همچنین در نظریهی احتمال و آمار برای محاسبهی احتمال وقوع رویدادهای خاص، که ترتیب وقوع آنها اهمیتی ندارد، استفاده میشوند. بهعلاوه، در مسائل انتخاب و گروهبندی، مانند انتخاب تیمها از بین یک مجموعه بزرگتر یا توزیع منابع بدون توجه به ترتیب، از ترکیب بهره گرفته میشود.
[برگرد بالا]
تعداد حالتهای انتخاب r (عدد صحیح و نامنفی) شیء از n (عدد صحیح و بزرگتر یا مساوی r) شیء را که ترتیب انتخاب اهمیت نداشته باشد، انتخاب r از n یا ترکیب r روی n گویند و به یکی از صورتهای زیر نمایش میدهند.
\[C(n,r) = C_r^n= \begin{pmatrix} n \\ r \end{pmatrix} \]
این عدد به ضریب دوجملهای نیز مشهور است که یکی از محلهای استفاده آن است.
بر اساس اصل ضرب از اصول شمارش، ترکیب دو عدد از رابطه زیر قابل محاسبه است.
\[\begin{pmatrix} n \\ r \end{pmatrix} = \frac{n!}{(n-r)!\cdot r!} \]
که منظور از !n، فاکتوریل عدد صحیح و نامنفی n است:
\[n! = n \times (n-1)! \;, \qquad 0! = 1 \]
\[n! = n \times (n-1) \times (n-2) \times \cdots \times 3 \times 2 \times 1 \]
ترکیب دو عدد کاربردهای بسیاری در محاسبات ریاضی دارد:
1- تعداد زیرمجموعههای r عضوی یک مجموعه n عضوی برابر (C(n, r است.
2- یکی از روشهای محاسبه دنباله اعداد کاتالان استفاده از رابطه زیر است:
\[C_n = \frac{1}{n+1} \begin{pmatrix} 2n \\ n \end{pmatrix} \]
3- ضرایب بسط دوجملهای نیوتن با استفاده از ترکیب محاسبه میشود:
\[{(a+b)}^n = \sum_{i=0}^{n} \begin{pmatrix} n \\ i \end{pmatrix} a^{n-i}b^i \]
4- تعداد جوابهای معادله سیاله (یا دیوفانت) X1 + X2 + X3 + ... + Xn = k با شروط Xi ≥ 0 و k ≥ 0 برابر با (C(n + k - 1, k است.
5- ...
هر کدام از این کاربردها و مباحث مرتبط، به بیانهای مختلف در سوالات مسابقات برنامهنویسی نیز به چشم میخورد. مسئله مربی ناامید نمونهای از این سوالات است.
[برگرد بالا]
با توجه به شرط n ≥ r ≥ 0، اگر ترکیب r روی هر n را در سطرهای زیر هم بنویسیم، جدولی مثلثی شکل به وجود میآید که به مثلث خیام - پاسکال مشهور است:
\[\begin{matrix} \begin{pmatrix}0\\0\end{pmatrix} & & & & \\ \begin{pmatrix}1\\0\end{pmatrix} & \begin{pmatrix}1\\1\end{pmatrix} & & & \\ \begin{pmatrix}2\\0\end{pmatrix} & \begin{pmatrix}2\\1\end{pmatrix} & \begin{pmatrix}2\\2\end{pmatrix} & & \\ \begin{pmatrix}3\\0\end{pmatrix} & \begin{pmatrix}3\\1\end{pmatrix} & \begin{pmatrix}3\\2\end{pmatrix} & \begin{pmatrix}3\\3\end{pmatrix} & \\ \begin{pmatrix}4\\0\end{pmatrix} & \begin{pmatrix}4\\1\end{pmatrix} & \begin{pmatrix}4\\2\end{pmatrix} & \begin{pmatrix}4\\3\end{pmatrix} & \begin{pmatrix}4\\4\end{pmatrix} \\ \vdots & \vdots & \vdots & \vdots & \vdots & \ddots \end{matrix} = \begin{matrix} 1 & & & & \\ 1 & 1 & & & \\ 1 & 2 & 1 & & \\ 1 & 3 & 3 & 1 & \\ 1 & 4 & 6 & 4 & 1 \\ \vdots & \vdots & \vdots & \vdots & \vdots & \ddots \end{matrix} \]
[برگرد بالا]
بر اساس تعریف فوق، ترکیب دو عدد با استفاده از تابع combination_1 در زبان برنامهنویسی ++C قابل محاسبه است:
long factorial(int n){
if( n == 0)
return 1;
return n * factorial(n - 1);
}
long combination_1(int n, int r){
long fn = factorial(n);
long fr = factorial(r);
long fnr = factorial(n - r);
return (fn / (fr * fnr));
}
محاسبه ترکیب دو عدد نیاز به محاسبه فاکتوریل سه عدد n ،n - r و r دارد. محاسبه این سه فاکتوریل از مرتبه اجرای خطی هستند. در نتیجه تابع combination_1 هم از مرتبه خطی
$\theta(n)$ است.
میزان رشد تابع فاکتوریل با افزایش مقدار ورودی آن بسیار زیاد است. به عنوان مثال، !10 یک عدد هفت رقمی و !100 یک عدد 158 رقمی است. در نتیجه امکان ذخیره کردن دقیق اعداد حاصل از فاکتوریل در متغیرهای معمول زبانهای برنامهنویسی ممکن نیست. این در حالی است که ترکیب دو عدد، علیرغم بزرگ بودن فاکتوریل ورودیهای آن، ممکن است عدد کوچکی باشد:
\[\begin{pmatrix}100\\99\end{pmatrix} = \frac{100!}{(100-99)! \times 99!} = \frac{100!}{99!}= 100 \]
یک راه حل آن است که در صورت نیاز با استفاده از توابع و کلاسها، ذخیرهسازی اعداد صحیح بزرگ را تعریف و مدیریت کنیم. در این حالت میتوان از بهینهسازی ضرب اعداد بسیار بزرگ و مسائل مربوطه هم استفاده کرد.
راه حل دیگر استفاده از رابطه زیر است که از تعریف فوق به راحتی قابل اثبات است:
\[\begin{pmatrix}n\\r\end{pmatrix} = \begin{pmatrix}n-1\\r\end{pmatrix} + \begin{pmatrix}n-1\\r-1\end{pmatrix} \qquad , \qquad \begin{pmatrix}n\\0\end{pmatrix} = \begin{pmatrix}n\\n\end{pmatrix} = 1 \]
این رابطه یک الگوریتم بازگشتی برای محاسبه ترکیب روی n بر اساس ترکیب روی n - 1 را نشان میدهد.
[برگرد بالا]
قطعه کد زیر رابطه فوق برای محاسبه ترکیب را به روش تقسیم و غلبه پیادهسازی میکند:
long combination_2(int n, int r){
if(n == r || r == 0)
return 1;
return (combination_2(n - 1, r) + combination_2(n - 1, r - 1));
}
این تابع فراخوانی بازگشتی را تا جایی ادامه میدهد که r برابر صفر یا n شود. در این حالت مقدار یک را باز میگرداند. پس میتوان گفت خروجی نهایی از جمع زدن (C(n, r تا عدد یک به دست میآید که به C(n, r) - 1 عمل جمع نیاز دارد. بنابراین نیاز به ذخیره کردن اعداد بسیار بزرگ وجود ندارد. اما این روش معایبی نیز دارد.
تعریف بازگشتی فوق به گونهای است که محاسبات تکراری وجود دارد. فراخوانی تابع به صورت (combination_2(n, r، دو فراخوانی (combination_2(n - 1, r و (combination_2(n - 1, r - 1 را به دنبال دارد. خود این دو فراخوانی هر کدام به صورت مجزا تابع را به صورت (combination_2(n - 2, r - 1 فراخوانی میکنند. یعنی (combination_2(n - 2, r - 1 دو بار به صورت تکراری محاسبه میشود. هر چقدر عمق فراخوانیهای بازگشتی بیشتر باشد، این تکرارها بیشتر میشود. چنین حالتی را در اصطلاح همپوشانی گویند.
ثابت شده است که برای محاسبه (C(n, r با تابع combination_2، تعداد C(n, r) * 2 - 1 بار تابع فراخوانی میشود. چنین عددی در بدترین حالت از مرتبه نمایی است که چندان قابل قبول نیست.
نکته: بدترین حالت این محاسبه زمانی است که r برابر بزرگترین عدد صحیح کوچکتر یا مساوی نصف n (یا به اصطلاح جزء صحیح n / 2) باشد. در این حالت به ازای یک n ثابت، (C(n, r بیشترین مقدار خود را دارد (چرا؟).
راه حلی که به نظر میرسد بتوان این همپوشانی را مهار کرد، ذخیره کردن محاسبات انجام شده در یک آرایه و استفاده مجدد از آنها در صورت نیاز است:
long comb[MAX][MAX] = { 0 };
long combination_3(int n, int r){
if(r == n || r == 0)
comb[n][r] = 1;
if(comb[n][r] == 0)
comb[n][r] = combination_3(n - 1, r) + combination_3(n - 1, r - 1);
return comb[n][r];
}
آرایه دو بعدی comb مقادیر ترکیب r روی n را در خود ذخیره میکند. در مقداردهی اولیه، تمامی عناصر آرایه را برابر صفر قرار میدهیم که مشخص میکند محاسبهای انجام نشده است. در هر بار فراخوانی تابع، مقدار [comb[n][r بررسی میشود. اگر این مقدار برابر صفر باشد، نشان میدهد [comb[n][r قبلا محاسبه نشده است. چرا که (C(n, r عدد مثبت و غیر صفر است. اما اگر مقدار آن غیرصفر باشد، این مقدار به عنوان نتیجه بازگشت داده میشود.
توجه: مقداردهی اولیه صفر به تمامی عناصر آرایه - یا حداقل قسمت مورد نیاز - خود یک فرآیند زمانبر است.
[برگرد بالا]
تابع combination_3 اگرچه محاسبات تکراری را انجام نمیدهد، اما همچنان فراخوانیهای بازگشتی تو در تو وجود داشته و سربار زمانی و حافظه ایجاد میکند. علت این مسئله در ذات روش تقسیم و غلبه و حل کل به جزء مسئله است. بر اساس روش برنامهنویسی پویا، مسئله را به صورت جزء به کل نیز میتوان حل کرد.
با توجه به جدول خیام - پاسکال، در روش کل به جزء و تقسیم و غلبه، با فراخوانیهای بازگشتی از (C(n, r به سمت مقادیر کوچکتر n حرکت کرده و با بازگشت مجدد از توابع، محاسبات انجام شده و مقدار (C(n, r به دست میآید. در روش جزء به کل و برنامهنویسی پویا، محاسبات از بالای جدول خیام - پاسکال به سمت پایین و محل (C(n , r انجام میشود. بنا به خاصیت مطرح شده برای ترکیب دو عدد، اعداد هر سطر از روی اعداد سطر بالاتر قابل محاسبه است. با پیشروی محاسبه این سطرها تا سطر nام - که (C(n, r در آن قرار دارد - محاسبه به پایان میرسد:
long combination_4(int n, int r){
int i, j;
for(i = 0 ; i <= n ; i++){
comb[i][0] = 1;
comb[i][i] = 1;
}
for(i = 2 ; i <= n ; i++)
for(j = 1 ; j <= i - 1 ; j++)
comb[i][j] = comb[i - 1][j] + comb[i - 1][j - 1];
}
return comb[n][r];
}
تابع combination_4 نه تنها مقدار (C(n, r که تمام ترکیبات (C(m, r با شرط n ≥ m را محاسبه و در آرایه comb ذخیره میکند. به عبارت دیگر، این تابع n + 1 سطر اول مثلث خیام - پاسکال را در آرایه comb ذخیره کرده و مقدار (C(n, r را به عنوان خروجی تابع بازمیگرداند. پیچیدگی زمانی این الگوریتم
$\theta(n^2)$ است (چرا؟).
اگر هدف صرفا پیدا کردن مقدار (C(n, r باشد، میتوان محاسبات را کمی محدودتر کرد. چرا که برای محاسبه (C(n, r نیاز به محاسبه تمام مقادیر سطرهای فوقانی مثلث خیام - پاسکال نیست:
long combination_5(int n, int r){
int i, j, min, max;
for(i = 0 ; i <= n - r ; i++)
comb[i][0] = 1;
for(i = 0 ; i <= r ; i++)
comb[i][i] = 1;
for(i = 2 ; i <= n ; i++){
min = (r + i - n > 1) ? (r + i - n) : 1;
max = (i - 1 < r) ? i - 1 : r;
for(j = min ; j <= max ; j++)
comb[i][j] = comb[i - 1][j] + comb[i - 1][j - 1];
}
return comb[n][r];
}
تعداد محاسبات حلقه داخلی این تابع برابر (r (n - r است که از شکل زیر نیز قابل استنباط است:
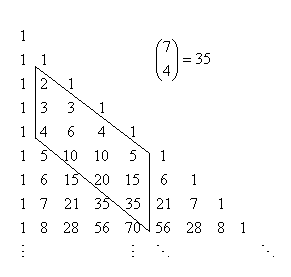
در نتیجه مرتبه اجرای آن $\theta(nr)$ است که در بدترین حالت به $O(n^2)$ منجر میشود.
این الگوریتم را از نظر حافظه مصرفی نیز میتوان بهینه کرد. همانگونه که بحث شد، هر سطر مثل خیام - پاسکال تنها به سطر قبلی خود وابسته است. بنابراین، اگر ذخیره کردن مقادیر غیر از (C(n, r اهمیت نداشته باشد، میتوان به جای آرایه دوبعدی و ذخیره کردن مقادیر سطرهای مختلف، از یک آرایه خطی برای ذخیره کردن سطر قبلی استفاده کرد. مقادیر سطر جدید را هم میتوان با شروع از انتهای سطر - و نه ابتدا - در همان آرایه محاسبه و ذخیره کرد. چنین الگوریتمی حافظه مصرفی را از
$\theta(n^2)$ به $\theta(n)$ کاهش میدهد:
long combination_6(int n, int r){
int i, j;
long comb[MAX];
for(i = 0 ; i <= n ; i++)
for(j = i ; j >= 0 ; j--)
if(j == 0 || j == i)
comb[j] = 1;
else
comb[j] = comb[j] + comb[j - 1];
return comb[r];
}