روش مرتبسازی سریع (Quick Sort) یکی از الگوریتمهای مشهور مرتبسازی دادهها است. این الگوریتم طی مراحل بازگشتی زیر یک روش تقسیم و غلبه برای مرتب کردن دادهها ارائه مینماید:
1- انتخاب عنصر محوری: یکی از عناصر آرایه به عنوان عنصر محوری (pivot) - به عنوان مثال عنصر اول - انتخاب میشود.
2- تقسیم آرایه: چینش عناصر آرایه به قسمی تغییر داده میشود که تمامی عناصر کوچکتر یا مساوی محور در سمت چپ آن و تمامی عناصر بزرگتر در سمت راست آن قرار بگیرند. این دو قسمت زیر آرایههای چپ و راست نامیده میشوند.
3- مرتبسازی بازگشتی: زیرآرایههای چپ و راست به روش مرتبسازی سریع مرتب میشوند.
[برگرد بالا]
با استفاده از تابع زیر - با فرض انتخاب عنصر اول به عنوان محور - میتوان مرحله تقسیم آرایه را پیادهسازی کرد:
int partition(int arr[], int low, int high){
int left = low + 1, right = high, temp, pivot = arr[low];
while(left <= right){
while(arr[left] <= pivot && left <= right)
left++;
while(arr[right] > pivot && left <= right)
right--;
if(left < right){
temp = arr[left];
arr[left] = arr[right];
arr[right] = temp;
}
}
arr[low] = arr[right];
arr[right] = pivot;
return right;
}
def partition(arr, low, high):
left, right, pivot = low + 1, high, arr[low]
while left <= right:
while arr[left] <= pivot and left <= right:
left += 1
while arr[right] > pivot and left <= right:
right -= 1
if left < right:
arr[left], arr[right] = arr[right], arr[left]
arr[low] = arr[right]
arr[right] = pivot
return right
تابع partition آرایه arr و اندیس بازه مورد نظر از آرایه جهت مرتبسازی را با low و high دریافت میکند. در متغیر pivot مقدار عنصر ابتدای بازه به عنوان عنصر محوری ذخیره میشود. همینطور در متغیر left اندیس عنصر دوم - اولین عنصر غیر محور بازه - و در متغیر right اندیس عنصر آخر ذخیره میشوند.
حلقه بیرونی تا زمانی که اندیس left کوچکتر یا مساوی اندیس right است تکرار خواهد شد. در این حلقه جابجاییهای لازم برای قرار گرفتن عنصر محوری در محل صحیح خود صورت میگیرد. حلقه درونی اول مقدار اندیس left را تا جایی که مقدار آن کمتر یا مساوی right بوده و مقدار عنصر متناظر آن در آرایه کمتر یا مساوی محور باشد افزایش میدهد. به همین ترتیب حلقه بعدی مقدار اندیس right را تا جایی که مقدار آن بیشتر یا مساوی left بوده و مقدار عنصر متناظر آن در آرایه بیشتر از عنصر محوری باشد کاهش میدهد. در انتها اگر left کوچکتر از right باشد مقدار متناظر آنها در آرایه جابجا میشود. چرا که بر اساس عملکرد دو حلقه درونی، اندیس left محل اولین عنصر بزرگتر از محور از ابتدای بازه و اندیس right محل اولین عنصر کوچکتر از محور از انتهای بازه را مشخص میکند. اگر این شرط برقرار نباشد به معنی آن است که تمامی عناصر بزرگتر از محور در سمت راست و تمامی عناصر کوچکتر از محور در سمت چپ بازه جمع شدهاند (چرا؟). در پایان مقدار محور با مقدار حد فاصل دو زیرآرایه جابجا شده و اندیس محل محور به عنوان محل تقسیم دو زیرآرایه از تابع بازگشت داده میشود.
این تابع را روی یک آرایه هفت عنصری از اعداد صحیح بررسی میکنیم:
3 0 6 1 7 2 5
تابع به صورت (partition(arr, 0, 6 فراخوانی میشود:
3 0 6 1 7 2 5: pivot = 3, left = 1, right = 6
شرط left < right برقرار است. پس وارد حلقه شده و حلقههای درونی اجرا میشوند. پس از اجرای حلقهها مقدار left و right به اندیس دو و پنج تغییر میکنند و مقادیر متناظر آنها جابجا میشوند:
3 0 2 1 7 6 5: pivot = 3, left = 2, right = 5
شرط left < right همچنان برقرار است. حلقههای درونی مقدار left و right را به چهار و سه تغییر میدهند. اما چون left < right نیست جابجایی انجام نمیشود:
3 0 2 1 7 6 5: pivot = 3, left = 4, right = 3
با نادرست بودن شرط left < right از حلقه بیرونی نیز خارج شده و به دستورات جابجایی نهایی میرسیم:
1 0 2 3 7 6 5
عنصر محوری جابجا شده است. در این حالت عدد سه به طور قطع در محل اصلی خود پس از مرتبسازی قرار دارد. چرا که تمامی عناصر زیرآرایه چپ از آن کوچکتر و تمامی عناصر زیرآرایه راست از آن بزرگتر هستند. این بازهها هر تغییری در چینش داشته باشند، تاثیری در محل عدد سه نخواهند داشت.
[برگرد بالا]
در مرحله بعدی از الگوریتم مرتبسازی سریع، دو زیرآرایه چپ و راست به صورت بازگشتی مرتب میشوند:
void quick_sort(int arr[], int low, int high){
if(low < high){
int pivot = partition(arr, low, high);
quick_sort(arr, low, pivot - 1);
quick_sort(arr, pivot + 1, high);
}
}
def quick_sort(arr, low, high):
if low >= high:
return
pivot = partition(arr, low, high)
quick_sort(arr, low, pivot - 1)
quick_sort(arr, pivot + 1, high)
تابع quick_sort آرایه و بازه مورد نظر برای مرتبسازی را دریافت کرده، پس از تقسیم آرایه و مشخص شدن محل عنصر محوری، دو زیرآرایه چپ و راست را با فراخوانی بازگشتی حل میکند. توجه داشته باشید که در این تابع pivot اندیس عنصر محوری را در خود ذخیره میکند. در تابع partition این متغیر مقدار عنصر محوری را ذخیره میکرد.
در مثال فوق وضعیت آرایه پس از اجرای دستور تقسیم آرایه در هر فراخوانی به صورت زیر خواهد بود:
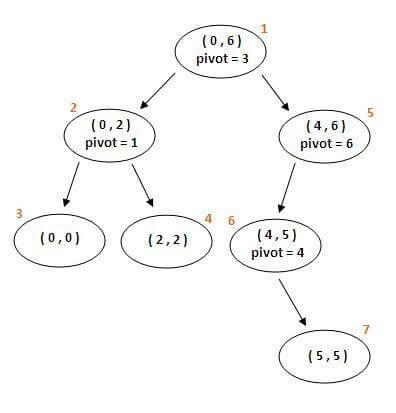
0) 3 0 6 1 7 2 5: low = 0, high = 6
1) quick_sort(arr, 0, 6 ) -> 1 0 2 3 7 6 5, pivot = 3
2) quick_sort(arr, 0, 2 ) -> 0 1 2 3 7 6 5, pivot = 1
3) quick_sort(arr, 0, 0 ) -> 0 1 2 3 7 6 5
4) quick_sort(arr, 2, 2 ) -> 0 1 2 3 7 6 5
5) quick_sort(arr, 4, 6 ) -> 0 1 2 3 5 6 7, pivot = 6
6) quick_sort(arr, 4, 5 ) -> 0 1 2 3 5 6 7, pivot = 4
7) quick_sort(arr, 5, 5 ) -> 0 1 2 3 5 6 7
در پایان آرایه مرتب شده است.
[برگرد بالا]
در مرتبسازیهای مبتنی بر مقایسه عموما تعداد مقایسهها ملاک بررسی پیچیدگی زمانی است. $T(n)$ را تعداد مقایسههای لازم برای مرتب کردن آرایهای به طول $n$ با روش مرتبسازی سریع در نظر میگیریم. تابع partition برای تقسیمبندی بازهای به طول $n$ به غیر از عنصر محوری تمامی عناصر را مقایسه میکند و به $n - 1$ مقایسه نیاز دارد.
بهترین حالت قرار گرفتن عنصر محوری زمانی است که این عنصر در وسط بازه قرار بگیرد و آن بازه را به دو بازه با اندازه تقریبا برابر تقسیم کند. در این حالت هر زیربازه $ T(\frac{n}{2}) $ مقایسه نیاز خواهد داشت و میتوان نوشت:
\[T(n) = 2 T(\frac{n}{2}) + n - 1 \]
با استفاده از قضیه اصلی یا حل رابطه بازگشتی مشخص میشود که $T(n)$ از مرتبه اجرای $ \theta (n log n)$ است.
در بدترین حالت عنصر محوری در یک سوی بازه قرار گرفته و تمامی عناصر دیگر در یک سمت آن جمع میشوند. این حالت زمانی اتفاق میافتد که بازه از قبل به صورت نزولی یا صعودی مرتب باشد. در نتیجه یک زیربازه از اندازه صفر و یک زیربازه از اندازه $n - 1$ تولید خواهد شد:
\[T(n) = T(0) + T(n - 1) + n - 1 = T(n - 1) + n - 1 \]
حل این رابطه بازگشتی نشان از مرتبه اجرایی $ \theta(n^2)$ در بدترین حالت اجرای الگوریتم دارد.
[برگرد بالا]
1- پیچیدگی زمانی اجرای الگوریتم در بهترین حالت $ \theta(n log n)$ و در بدترین حالت $ \theta (n^2)$ است. با استفاده محاسبات ریاضی میتوان نشان داد در حالت متوسط نیز مرتبه اجرا $ \theta (n log n)$ است.
2- این الگوریتم یک مرتبسازی درجا است. یعنی میزان حافظه مصرفی الگوریتم مستقل از طول آرایه است.
3- زمانی که تعداد عناصر آرایه کم باشد، سرعت اجرای مرتبسازی درجی بهتر از مرتبسازی سریع است. به همین دلیل طی مراحل بازگشتی مرتبسازی سریع، اگر طول بازه عدد کوچکی باشد، معمولا بازه با مرتبسازی درجی مرتب میشود.
4- الگوریتم مرتبسازی سریع با پیادهسازی فوق یک روش ناپایدار است. چنین الگوریتمی لزوما ترتیب عناصر با مقدار یکسان را پس از مرتبسازی حفظ نمیکند.
5- انتخاب عنصر محوری بحث مفصلی دارد. اما در کل یک انتخاب آزاد است. میتوان عنصر اول، عنصر آخر، یا هر عنصر دیگری را به عنوان عنصر محوری انتخاب کرد. حتی لازم نیست از ابتدا تا انتها از یک روش انتخاب استفاده کرد. یکی از روشهای رایج، انتخاب یک عنصر تصادفی به عنوان عنصر محوری است. اگرچه انتخاب عنصر محوری مناسب باعث بالا رفتن کارایی الگوریتم میشود، اما عموما هزینه لازم برای یافتن چنین محوری بالا بوده و مقرون به صرفه نیست.