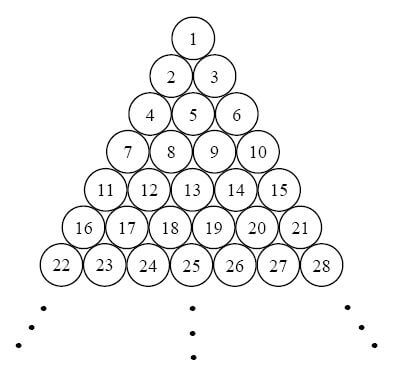
دو دوست در زمین نامحدودی متشکل از حصارهای دایرهای شکل هماندازه با ساختار زیر قرار دارند. یکی از دوستان قصد دارد با حرکت در این ساختار نزد دوست دیگر خود برود. حرکت در این ساختار در هر گام شامل جابجایی به یکی از دایرههای مجاور است. دو دایره مجاور هستند اگر در یک نقطه مشترک باشند.
با توجه به موقعیت دو دوست در این ساختار، هدف یافتن حداقل گامهای مورد نیاز برای رسیدن دو دوست به یک خانه است. توجه داشته باشید که محل اولیه دو دوست لزوما متمایز نبوده و در کل مراحل یک دوست در محل خود ثابت مانده و دوست دیگر حرکت میکند.
ورودی برنامه
[برگرد بالا]
هر ورودی در یک سطر نوشته شده است که شامل دو عدد صحیح به عنوان مختصات دو دوست (مطابق شکل فوق) است. انتهای ورودی با دو عدد صفر (یعنی 0 0) مشخص میشود.
1 3
2 6
23 9
0 0
خروجی برنامه
[برگرد بالا]
خروجی برای هر سطر از ورودی شامل حداقل گامهای مورد نیاز برای کنار هم قرار گرفتن دو دوست است.
1
2
4
منبع: مسابقه ICPC منطقهای آسیا 2009 - سایت تهران -
مسئله Best Friends
حل مسئله
[برگرد بالا]
سوای مختصات عددی مشخص شده برای دایرهها، هر دایره را میتوان با سه ویژگی شماره سطر، شماره قطر اصلی و شماره قطر فرعی مشخص کرد:
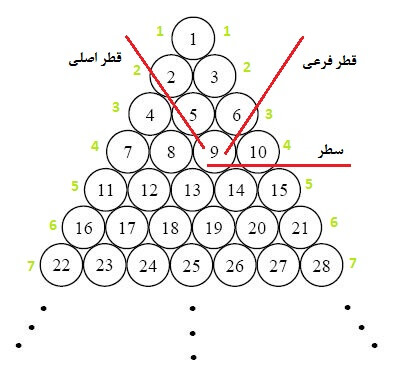
اگر دو دایره در یک سطر یا یک قطر اصلی یا یک قطر فرعی قرار داشته باشند، حرکت فقط روی سطر یا قطر اصلی یا قطر فرعی صورت گرفته و محاسبه حداقل گام حرکت بسیار آسان است. اما اگر اینگونه نباشد، حرکت به سمت دایره مبدأ فقط به دو نوع حرکت از سه نوع حرکت سطری و قطری نیاز دارد (چرا؟).
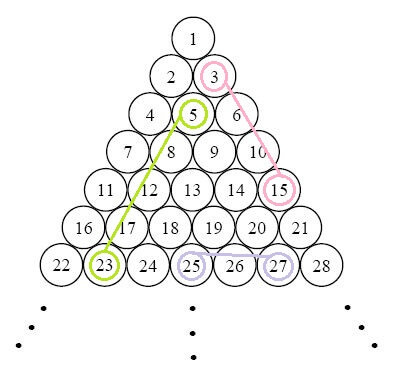
این انتخاب که کدام حرکتها انتخاب شود، بسته به میزان اختلاف سطری و قطری دو دایره دارد. از میان اختلافها دو اختلافی که کوچکتر هستند انتخاب شده و حرکت طی آن مسیرها انجام میشود. در نتیجه مجموع آنها به عنوان حداقل گام مورد نیاز به دست میآید.
به عنوان مثال، اگر دو دوست در دایرههای 5 و 19 قرار داشته باشند، اختلاف سطری و قطر اصلی و قطر فرعی آنها به ترتیب اعداد 3، 1 و 2 است. بنابراین مسیر حرکت قطر اصلی و قطر فرعی با طول گامهای 3 انتخاب میشود که کوتاهترین راه ممکن است.
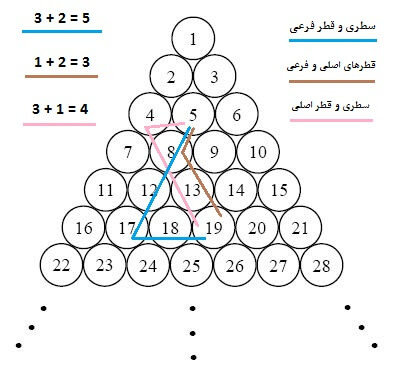
توجه داشته باشید که در حالت کلی مهم نیست کدام حرکت ابتدا انجام شود. در مثال فوق میتوان ابتدا در راستای قطر فرعی و سپس در راستای قطر اصلی حرکت کرد. گاهی اوقات ساختار مثلثی شکل زمین اجازه یکی از این حرکتهای یکسان را نمیدهد.
تنها نکته باقیمانده نحوه محاسبه شماره سطر و قطرهای هر دایره است. بر اساس ساختار شمارهگذاری دایرهها در شکل فوق، اعداد سطر شماره R بین اعداد $ 1 + \frac{R \times ( R - 1 )}{2} $ و $ \frac{R \times ( R + 1 )}{2} $ است. پس میتوان با یک حلقه تکرار، عدد R را به نحوی که n بین این دو عدد قرار بگیرد پیدا کرد. البته این نامساوی را میتوان با استفاده از روابط ریاضی حل کرده و به روش مستقیم مقدار R را از روی n محاسبه کرد. علاقهمندان میتوانند آن رابطه را نبز به دست بیاورند.
شماره قطر اصلی و فرعی نیز به ترتیب از جمع عدد یک با تفاضل عدد دایره (همان n) و بزرگترین شماره موجود در سطر و تفاضل عدد دایره از کوچکترین شماره موجود در سطر به دست میآید. مثلا عدد 19 در سطر 6 قرار دارد. چرا که رابطه 16 ≤ 19 ≤ 21 برقرار است. شماره قطر اصلی برابر 1 + 19 - 21 = 3 و شماره قطر فرعی برابر 1 + 16 - 19 = 4 است.
نکته آخر اینکه چنین روشی حالتی را که دو دایره در یک سطر یا قطر قرار دارند پوشش میدهد و نیازی به بررسی جداگانه آن حالتها نیست.