یکی از مسائل جالب طراحی الگوریتم مسئله کاشیکاری یا فرش کردن زمین با موزاییک است. فرض کنید قطعه زمین مربعی شکل با ابعادی از توان عدد دو داریم. هدف فرش کردن این قطعه زمین با استفاده از موزاییکهایی با شکل L است به قسمی که یکی از خانههای زمین شطرنجی شده فوق پوشیده نشود. میتوان فرض کرد از این خانه برای احداث باغچه یا حوضچه کوچکی استفاده خواهد شد. در ضمن حق شکستن این موزاییکها به تکههای کوچکتر را نداریم.
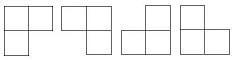
به عنوان مثال، فرض کنید زمینی با ابعاد چهار متر داریم که میخواهیم خانه مشخص شده زیر پوشیده نشود:

میتوان این زمین را به صورت زیر فرش کرد:
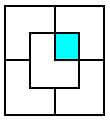
اما راه حل کلی مسئله چیست؟
با توجه به اینکه ابعاد زمین توانی از عدد دو است، روش تقسیم و حل را برای پوشانیدن این قطعه زمین امتحان میکنیم. بر اساس تعریف روش تقسیم و حل، باید بتوان مسئله را به زیرمسائلی از نوع خود مسئله تقسیم کرد و با ادغام نتایج حاصل از آنها، به نتیجه اصلی دست پیدا کرد. چون ابعاد این قطعه زمین توانی از عدد دو است، پس میتوان آن را به دو قسمت تقسیم کرد. با تقسیم طول و عرض زمین به دو قسمت، چهار قطعه زمین کوچکتر به دست میآید:

اما همه این چهار قطعه زمین شرایط مسئله اصلی را دارا نیستند. در صورت مسئله عنوان شده است که باید از پوشانیدن یکی از خانههای قطعه زمین صرف نظر کرد. از چهار قطعه زمین کوچکتر تنها یکی از آنها این شرط را برآورده میکند و بقیه قطعه زمینها باید به طور کامل پوشانیده شوند. این نقص را میتوان با به کار بردن یک موزاییک حل کرد:

این موزاییک در مرکز قطعه زمین به قسمی قرار داده شده است که هر کدام از سه قسمت مربعی شکل آن، داخل یکی از قطعه زمینهای کوچکتری قرار گرفته است که شرط مسئله را برآورده نمیکردند. با این کار، داخل این قطعه زمینها نیز خانهای وجود دارد که نباید پوشانیده شود. چرا که از قبل توسط موزاییکی پوشیده شده است. به این ترتیب همه چهار قطعه زمین کوچکتر خانهای دارند که نیاز به پوشش ندارد. در نتیجه میتوان بر روی حل مسئله در قطعه زمینهای کوچکتر تمرکز کرد:

اگر قطعه زمینهای کوچکتر از ابعاد دو باشند، به سادگی با قرار دادن یک موزاییک میتوان آن را پوشانید:

پس به طور خلاصه، برای حل مسئله باید به این صورت عمل کنیم:
قطعه زمین را از طول و عرض به دو قسمت تقسیم میکنیم. با این تقسیمات چهار قطعه زمین کوچکتر حاصل میشود. تکه مربعی شکل کوچکی که نباید پوشانیده شود داخل یکی از این قطعه زمینهای کوچکتر قرار خواهد گرفت. یک موزاییک را در مرکز قطعه زمین طوری قرار میدهیم که هر کدام از سه قطعه زمین کوچکتر دیگر یک قسمت از موزاییک را در خود داشته باشند. به این ترتیب چهار قطعه زمین کوچکتر به دست میآید که در هر کدام از آنها خانهای وجود دارد که نباید پوشانیده شود. ابعاد آنها نیز به طور حتم عددی از توان دو است. در نتیجه میتوان از همین روش برای پوشانیدن آنها استفاده کرد. تقسیمات متوالی قطعه زمینها به تکههای کوچکتر تا زمانی ادامه پیدا میکند که به قطعه زمینهایی با ابعاد دو متر برسیم. در این حالت به سادگی میتوان با یک موزاییک زمین را به طور کامل پوشش داد.

[برگرد بالا]
یکی از سوالات مهم این است که برای پوشانیدن قطعه زمین با توجه به شرایط مسئله چند موزاییک لازم است؟
فرض کنید $ T(n) $ تعداد موزاییکهای لازم برای پوشانیدن زمینی با ابعاد n باشد. با توجه به استفاده از روش تقسیم و حل، هر قطعه زمین به چهار قطعه زمین با ابعاد نصف تبدیل میشود. اما برای این تبدیل از یک موزاییک استفاده میکنیم. پس میتوان نوشت:
\[ T( n ) = 4 T( \frac{n}{2} ) + 1 \]
اگر ابعاد قطعه زمین دو متر باشد، تنها یک موزاییک برای پوشانیدن آن کافی است:
\[ T( 2 ) = 1 \]
پس میتوان گفت تعداد موزاییکهای لازم برای پوشش زمینی با ابعاد n از رابطه بازگشتی زیر به دست میآید:
\[ T( n ) = 4 T( \frac{n}{2} ) + 1 \qquad , \qquad T( 2 ) = 1 \]
با حل این رابطه بازگشتی با استفاده از روشهای متعارف ریاضی نتیجه زیر حاصل میشود:
\[ T( n ) = \frac{n^2 - 1}{3} \]
برای محاسبه $ T(n) $ راه سادهتری هم وجود دارد. در داخل قطعه زمینی با ابعاد n، تعداد n2 خانه مربعی شکل وجود دارد. یکی از این خانهها نباید پوشانیده شود. پس n2 - 1 خانه مربعی شکل کوچک داریم که باید توسط موزاییکها پوشانیده شوند. هر موزاییک نیز سه خانه مربعی شکل کوچک را پوشش میدهد. پس در مجموع به $ \frac{n^2 - 1}{3} $ موزاییک نیاز خواهیم داشت.