الگوریتمستان - معمای هشت وزیر

معمای هشت وزیر از جمله مسائل کلاسیک مباحث طراحی الگوریتم است که در حالت کلی‌تر با عنوان معمای n وزیر یا معمای چند وزیر مطرح می‌شود.

  

برای افرادی که با بازی شطرنج آشنایی ندارند

  [برگرد بالا]

وزیر مهره‌ای از مهره‌های بازی شطرنج است که می‌تواند در تمامی هشت جهت به هر تعداد خانه - تا زمانی که مهره‌ای مانع نباشد - حرکت کند. اگر در این مسیرها مهره‌ای از حریف قرار گرفته باشد، آن مهره در معرض خطر حمله توسط وزیر قرار دارد؛ یا به اصطلاح وزیر آن مهره را تهدید می‌کند.

  

  

معمای n وزیر

  [برگرد بالا]

هدف از مسئله هشت وزیر، چیدن 8 مهره وزیر روی یک صفحه شطرنج خالی است، به قسمی که هیچ مهره‌ای مهره‌های دیگر را تهدید نکند. به عبارت دیگر، 8 وزیر باید به نحوی چیده شوند که هیچ‌کدام در بک سطر، بک ستون یا بک قطر قرار نداشته باشند. یک جواب مسئله می‌تواند به صورت زیر باشد:

  

  

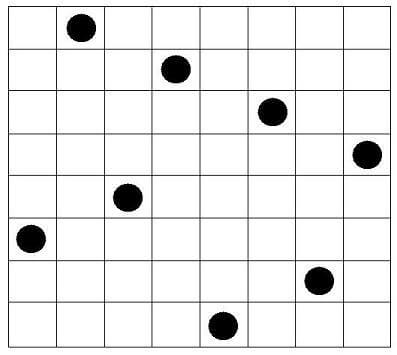
در حالت کلی به جای عدد 8 از عدد طبیعی $n$ استفاده شده و مسئله به ازای هر $n$ بزرگتر یا مساوی 4 مورد بررسی قرار می‌گیرد. به این ترتیب، هدف مسئله چیدن $n$ مهره وزیر در یک صفحه شطرنج با ابعاد $n \times n $است.

در یک صفحه $n$ در $n$ تعداد $n^2$ خانه وجود دارد که از بین آنها $n$ خانه برای قرار گرفتن $n$ وزیر انتخاب می‌شود. در این انتخاب‌ها ترتیب اهمیتی ندارد. پس تعداد حالت‌های انتخاب $n$ خانه برای چیدن $n$ وزیر ترکیب $n$ از $n^2$ یا $ C(n^2, n) $ است که حتی برای $n‌$ های نه چندان بزرگ (نظیر 8) عدد بزرگی به دست می‌آید. در نتیجه بررسی تمامی حالات ممکن چینش مهره‌ها برای رسیدن به چیدمان صحیح به هیچ عنوان مقرون به صرفه نیست. از سوی دیگر به ازای هر $n$، تنها یک جواب منحصربفرد وجود ندارد. بنابراین اگر هدف مسئله یافتن تمامی جواب‌های ممکن باشد، استفاده از روش‌های هوشمند تکاملی یا الگوریتم‌های جستجوی تصادفی، لزوما ما را به نتیجه مطلوب نمی‌رساند.

  

روش عقبگرد

  [برگرد بالا]

یکی از روش‌های حل این مسئله، استفاده از راهبرد عقبگرد است. در این روش تمام فضای مسئله به صورت یک درخت در نظر گرفته می‌شود که سطح $i$ام شامل تمام انتخاب‌های مهره $i$ام است. با توجه شرایط مسئله در هر سطر از صفحه شطرنج تنها یک مهره می‌تواند قرار بگیرد. به این ترتیب سطح شماره $i$، محل مهره iام در سطر شماره$i$ صفحه شطرنج را مشخص می‌کند. قسمتی از چنین درختی به ازای $n = 4$ به این صورت خواهد شد:

  

  

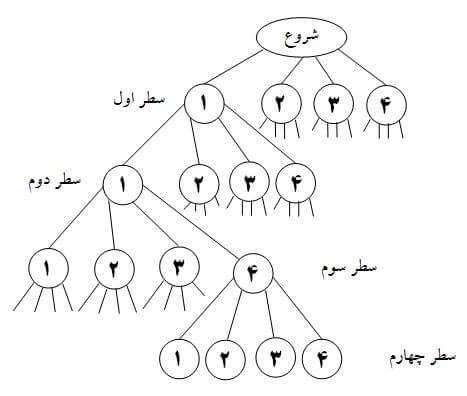
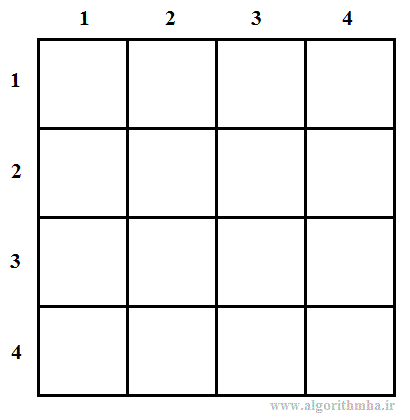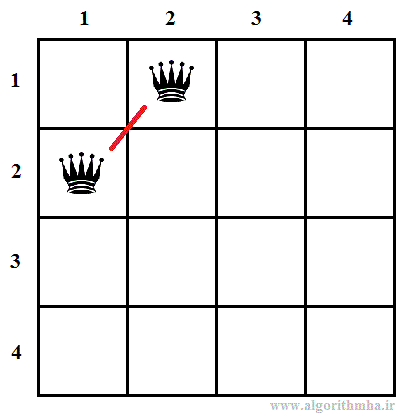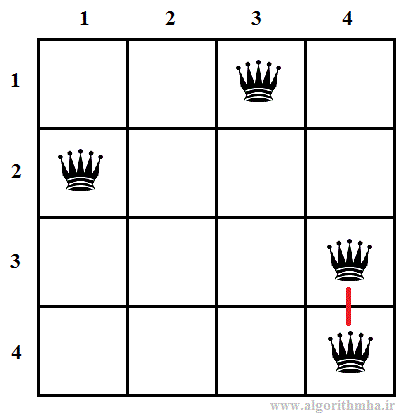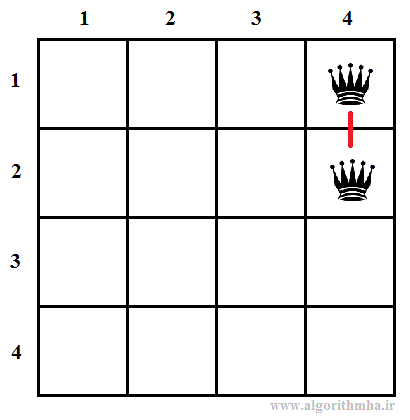
پیمایش پیشوندی (PreOrder) چنین درختی تمام حالت‌های فضای مسئله را برای یافتن پاسخ جستجو می‌کند. اما حین پیمایش می‌توان از پیمایش گره‌های غیرامیدبخش صرف‌تظر کرد. گره‌های غیرامیدبخش گره‌هایی هستند که بر اساس تعاریف مسئله می‌توان مطمئن بود هرگز به جواب درست نمی‌رسد. به عنوان مثال، اگر با گره 1 در سطح یک شروع کرده و به گره 1 در سطح دو برویم، این گره امیدبخش نیست. چرا که دو مهره اول در ستون شماره یک چیده شده‌اند و یکدیگر را تهدید می‌کنند. این اتفاق مستقل از این که مهره‌های بعدی در چه محل‌هایی قرار بگیرد مطمئنا به جواب صحیح ختم نمی‌شود. در نتیجه از پیمایش فرزندان گره شماره 1 در سطح دوم صرف نظر کرده و روال را با فرزند بعدی گره والد آن - یعنی گره شماره 2 در سطح دوم - ادامه می‌دهیم. به همین ترتیب این گره نیز امیدبخش نیست. چرا که در چنین حالتی مهره در ستون شماره 2 از سطر دوم قرار می‌گیرد که با وزیر سطر اول و ستون 1 در یک قطر قرار دارند.

چنین پیمایشی معادل این است که از بالای صفحه شطرنج (سطر اول) شروع کرده و مهره را در ستون شماره 1 قرار بدهیم. اگر چینش این مهره با مهره‌های بالاتر تهدیدی ایجاد نکند، چینش مهره بعدی در سطر بعدی را با همین روش ادامه می‌دهیم. اما اگر تهدیدی اتفاق بیفتد، مهره را یک خانه به سمت راست جابجا می‌کنیم. اگر مهره به انتهای سطر رسیده باشد، آن مهره را برداشته و مهره سطر بالاتر را یک خانه به سمت راست جابجا می‌کنیم. اگر حین پیش‌روی سطرها به سمت پایین، به انتهای صفحه برسیم، یک جواب از مسئله تولید شده است.

  

  

پیاده‌سازی مسئله

  [برگرد بالا]

یکی از مهم‌ترین بخش‌های پیاده‌سازی مسئله 8 وزیر، روش بررسی تهدید مهره‌ها است.

یک روش این است که یک آرایه دو بعدی n در n به عنوان صفحه شطرنج تعریف شود. با مشخص شدن محل هر مهره، تمام خانه‌هایی که توسط آن تهدید می‌شوند علامت‌گذاری می‌شود، تا بررسی غیرامن بودن آنها در مراحل بعدی آسان باشد. این روش در ابتدا بدون مشکل به نظر می‌رسد. اما سوای بحث مصرف حافظه، یک مشکل اساسی دیگر نیز وجود دارد. زمانی که تشخیص می‌دهیم فرزندان یک گره همه غیرامیدبخش هستند، از آن گره صرف نظر کرده و به گره بعدی فرزند والد مراجعه می‌کنیم. در نتیجه باید محل مهره در آن سطر جابجا شده و محل‌های غیرامنی که علامت‌گذاری شده بودند به حالت قبل از علامت‌گذاری بازگردند. اما مسئله اینجاست که محل‌های علامت‌گذاری شده پس از جابجایی لزوما امن نمی‌شوند. ممکن است همچنان توسط مهره دیگری تهدید وجود داشته باشد. تشخیص این مسئله که آیا آن محل به صورت امن مشخص شود یا نه، زمان مصرفی الگوریتم را دو چندان می‌کند.

در روش دوم، تنها محل قرار گرفتن هر مهره به صورت شماره سطر و ستون ذخیره می‌شود. این ذخیره‌سازی می‌تواند در یک آرایه یک بعدی باشد. به این ترتیب که شماره اندیس آرایه، شماره سطر مهره را مشخص کرده و مقدار آن، شماره ستون مهره باشد. مثلا اگر مقدار اندیس شماره 1 آرایه 4 باشد، یعنی وزیر سطر اول در خانه چهارم قرار دارد. پس از این تعریف، با مشخص شدن محل یک مهره جدید، خانه‌هایی که ممکن است این خانه را تهدید کنند بررسی می‌شوند، تا امن بودن آن مشخص شود. مزیت این روش به روش قبلی - علاوه بر مصرف کمتر حافظه - رفع مشکل بررسی محل‌های علامت‌گذاری شده است.

برای بررسی این مسئله که آیا محل مهره جدید تهدیدی ایجاد می‌کند یا نه، به جای بررسی تک‌تک خانه‌های ستونی و قطری، از روابط ریاضی استفاده می‌شود. یافتن پاسخ این سوال که آیا در ستونی که مهره قرار دارد، قبلا مهره‌ای قرار داده شده است یا نه، کار چندان دشواری نیست. کافی است یک آرایه یک بعدی به طول n تعریف شده و هرگاه مهره‌ای در یک ستون مستقر شد، شماره ستون آن در آرایه به عنوان غیرامن علامتگذاری شود. در نتیجه مثلا اگر مهره جدید در ستون شماره 3 قرار گرفت، کافی است اندیس شماره 3 این آرایه برای اطمینان از امن بودن این ستون بررسی شود.

در مورد دو قطر راست و چپ موضوع کمی پیچیده به نظر می‌رسد. اما با کمی دقت، یک رابطه ثابت ریاضی برای هر یک از قطرها وجود دارد. مثلا تفاضل شماره ستون از شماره سطر تمامی خانه‌های روی قطر اصلی صفحه صفر است. یا مجموع شماره سطر و ستون تمامی خانه‌های قطر فرعی صفحه عدد 9 است. به همین ترتیب سایر قطرها نیز رابطه ریاضی مشابه دارند. در نتیجه مثلا اگر مهره جدید در سطر سوم و ستون دوم قرار گرفته باشد، تنها کافی است در مهره‌های چیده شده قبلی دنبال مهره‌ای باشیم که تفاضل ستون از سطر آن عدد 1، یا مجموع آنها عدد 5 باشد. اگر چنین مهره‌ای یافت نشد، تهدیدی از طرف قطرها وجود ندارد. راه بهتر آن است که آرایه‌ای به طول 2n - 1 برای دو قطر راست و چپ تعریف کرده و اگر مهره‌ای در یک قطر مستقر شد، آن قطر به عنوان قطر ناامن در آرایه علامتگذاری شود. در مرحله بعدی با قرار گرفتن هر مهره جدید، به جای بررسی تمام خانه‌های مهره‌های قبلی، این دو آرایه بررسی شوند. چنین آرایه‌هایی بر خلاف روش علامت‌گذاری قبلی، مشکل حذف علامت‌ها را ندارد (چرا؟).

  

  

  

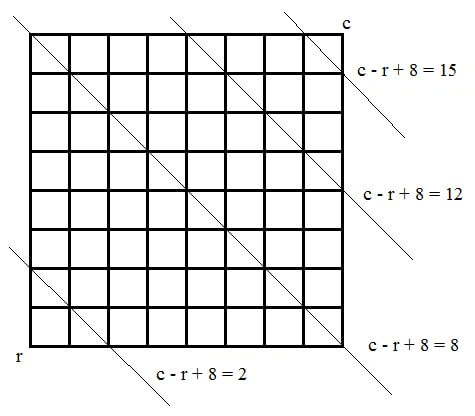
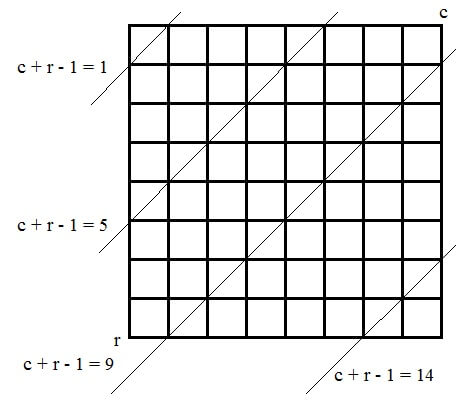
نکته: با توجه به اینکه در قسمت پایین قطر اصلی تفاضل شماره ستون از شماره سطر عدد منفی می‌شود، برای حفظ استاندارد شروع از یک، آن را با عدد n جمع می‌زنند. همینطور در مورد مجموع شماره سطر و ستون، عدد یک کسر می‌شود.

  

روش‌های دیگر حل مسئله

  [برگرد بالا]

همانگونه که عنوان شد، روش عقبگرد تمامی جواب‌های مسئله را تولید کرده و با صرف نظر کردن از گره‌های غیرامیدبخش بهینگی قابل توجهی در زمان اجرای الگوریتم ایجاد می‌کند. اما با افزایش مقدار $n$ و افزایش عمق درخت و تعداد فرزندان هر گره، سرعت اجرا نیز به صورت شبه‌نمایی افزایش یافته و کارایی روش پایین می‌آید.

اگر هدف از حل مسئله تنها رسیدن به یک جواب باشد، روش‌های دیگری وجود دارد که کارایی بهتری دارند. این روش‌ها عموما از چیدمان تصادفی یا شبه‌تصادفی (تصادفی هوشمند) برای رسیدن به یک جواب استفاده می‌کنند. اکثر الگوریتم‌های مکاشفه‌ای و فرا مکاشفه‌ای - مانند الگوریتم تکاملی ژنتیک - در این حالت جوابگوی نیازها هستند.