تعریف الگوریتم آنلاین در ویکیپدیا به این صورت است: «در علوم رایانه الگوریتم بَرخط به الگوریتمی اطلاق میشود که ورودی آن به صورت دنبالهای از تقاضاها در دسترس الگوریتم قرار میگیرد. به عبارت دیگر، ورودی این الگوریتمها از ابتدا در اختیار الگوریتم نیست. برای پردازش هر قطعه از ورودی، الگوریتم برخط تصمیمی غیرقابلبرگشت میگیرد». بر اساس این تعریف، هر الگوریتم حریصانه یک نوع الگوریتم آنلاین است. چرا که در راهحلهای حریصانه هم در هر مرحله یک تصمیم غیرقابل بازگشت بر اساس گزینههای موجود در آن لحظه گرفته میشود. همینطور الگوریتم مرتبسازی درجی یک نوع الگوریتم آنلاین است که با اضافه شدن هر داده بلافاصله محل آن در لیست مرتبشده مشخص میگردد.
برخی از الگوریتمهای آنلاین مستقل از کارایی به یک خروجی درست ختم میشوند. به عنوان مثال میدانیم همیشه خروجی مرتبسازی درجی یک لیست مرتب و خروجی الگوریتم پریم یک درخت پوشای کمینه است. اما در مقابل الگوریتمهایی مانند راه حل حریصانه برای مسئلهی کولهپشتی صفر-یک نیز پیشنهاد میشوند که خروجی آنها لزوما درست نیست اما شاید بتوانیم تصمیمهایی در هر مرحله بگیریم که امید بیشتری برای موفقیت داشته باشیم.
شاید برای شما هم پیش آمده باشد که در یک سفر بین شهری بخواهید از سرویسهای بهداشتی بین راه استفاده کنید. اما از وضعیت نظافت سرویسهای طول مسیر اطلاع ندارید و مشخص نیست اگر از یک سرویس بگذرید، آیا امیدی هست محل مناسبتر دیگری پیدا شود؟ در واقع سوال این است که چقدر احتمال دارد بهترین و تمیزترین سرویس بهداشتی را از بین گزینههای ممکن انتخاب کرده باشیم و حداقل چطور میتوانیم مطمئن شویم که با احتمال بالایی انتخاب خوبی داشتهایم؟ چالش مهم این نوع مسائل انتخاب بهتر از بین گزینههایی است که به صورت جریانی از اطلاعات یک به یک در اختیار ما قرار میگیرند و اگر گزینهای را رد کنیم امکان بازگشت وجود ندارد.

مثال فوق یک نمونه از مسائلی است که در حل آنها میتوان از الگوریتمهای آنلاین استفاده کرد. فرض کنید در مثال فوق فقط دو حق انتخاب داشته باشیم. در این حالت چه اولی را انتخاب کنیم و چه دومی را، با احتمال یک دوم انتخاب درستی داشتهایم و نیاز به استراتژی خاصی برای انتخاب نیست. اگر امکان انتخاب از بین سه گزینه باشد، شش ترتیب مختلف زیر از نظر نظافت وجود دارد که منظور از ۱ تمیزترین و منظور از ۳ کثیفترین سرویس بهداشتی است.
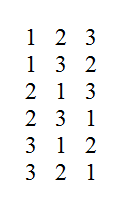
اگر یکی از این سرویسهای بهداشتی را به تصادف انتخاب کنیم با احتمال یک سوم انتخاب درستی کردهایم. حال این استراتژی را در نظر بگیرید که تمیزی گزینهی اول را بررسی کرده و بدون انتخاب آن، گزینهی دوم را به شرطی انتخاب کنیم که از اولی تمیزتر باشد. اگر نه، سراغ آخرین سرویس بهداشتی برویم. اجرای این استراتژی روی شش حالت بالا نتیجهی زیر را دارد که عدد پررنگ انتخاب ما بر اساس استراتژی است.
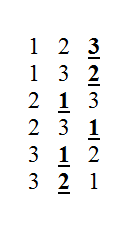
همانگونه که مشخص است، از شش حالت در سه حالت عدد ۱ (تمیزترین مکان) پررنگ شده است. پس اجرای این استراتژی با احتمال یک دوم انتخاب درستی برای ما دارد که از انتخاب تصادفی (یک سوم) بهتر است.
در حالت کلی ثابت میشود اگر $n$ گزینه وجود داشته باشد و $ n / e$ گزینهی اول (منظور از $e$ عدد نپر است) را بدون انتخاب رد کرده و در ادامه اولین گزینهای که از همهی گزینههای قبلی بهتر بود انتخاب کنیم، بیشترین احتمال موفقیت وجود دارد. با اضافه شدن به تعداد گزینهها احتمال موفقیت کوجکتر میشود، اما این احتمال از ۰٫۳۶۷۹ (و به صورت دقیقتر وارون عدد نپر) پایینتر نمیرود. یعنی با این استراتژی در بدترین شرایط با احتمال نزدیک به ۳۷ درصد بهترین سرویس بهداشتی انتخاب میشود.
احتمال ۳۷ درصد (حدود یک سوم) در وهلهی اول جذاب نیست. اما اگر در مسیر سفر ۱۰۰ سرویس بهداشتی وجود داشته باشد، از احتمال یک صدم برای انتخاب تصادفی بسیار بهتر است! همینطور اگر دومین تمیزترین سرویس هم برای ما قابل قبول باشد، این الگوریتم با احتمال بیش از یک دوم ما را به مقصود خواهد رساند! قطعه کد زیر به زبان پایتون احتمال موفقیت را بر اساس تعداد سرویسها و حداکثر رتبهی بهداشتی قابل قبول محاسبه میکند.
from random import shuffle
import math
max_acceptable_rank = 2
n_WC = 1000
sample_count = 100000
ranks = list(range(1, n_WC + 1))
threshold = int(n_WC / math.e)
succeed_count = 0
for _ in range(sample_count):
shuffle(ranks)
best = min(ranks[:threshold])
for i in range(threshold, n_WC):
if ranks[i] < best:
final_choice = ranks[i]
break
else:
final_choice = ranks[-1]
if final_choice <= max_acceptable_rank:
succeed_count += 1
print(succeed_count / sample_count)