یکی از روش‌های پرکاربرد و محبوب برای طراحی الگوریتم‌ها روش Divide and Conquer است که در زبان فارسی به صورت الگوریتم‌های تقسیم و حل یا تقسیم و غلبه ترجمه شده است.
در این روش، داده‌ها به دو یا چند دسته تقسیم شده و حل می‌شوند. سپس با ترکیب مناسب نتایج به دست آمده از این زیرمسئله‌ها، مسئله اصلی حل میشود. در صورتی که زیرمسئله خود به اندازه کافی بزرگ باشد، می‌توان از همین روش برای حل آن استفاده کرد. تقسیمات متوالی زیرمسئله‌ها تا جایی ادامه پیدا می‌کند که به اندازه کافی کوچک شده باشند و بتوان آنها را با روش‌های دیگر به راحتی حل نمود.
برای آشنایی بیشتر، چند الگوریتم که با روش حل و تقسیم پیاده‌سازی شده‌اند معرفی می‌شوند.
[برگرد بالا]
در روش مرتب‌سازی سریع داده‌های ورودی را بر حسب یکی از عناصر به نام محور به دو قسمت نه لزوما هم‌اندازه تقسیم کرده و هر کدام را جداگانه مرتب میکنیم.
[برگرد بالا]
در این روش نیز همانند روش مرتب‌سازی سریع داده‌ها به دو قسمت تقسیم می‌شوند. اما روش تقسیم کردن داده‌ها متفاوت است. طوری که قسمت‌های به دست آمده از تقسیم تقریبا هم‌اندازه هستند. پس از مرتب کردن زیر آرایه‌ها، با ادغام آنها آرایه اصلی به صورت مرتب‌شده حاصل میشود.
[برگرد بالا]
روش ضرب استراسن برای بهینه کردن عمل ضرب ماتریس‌ها توسط شخصی به نام استراسن معرفی شده است. در این روش هر کدام از ماتریس‌ها به چهار زیرماتریس تقسیم شده و عملیات ضرب با استفاده از آنها و رابطه‌هایی که استراسن عنوان کرده انجام میشود. با استفاده از این روش مرتبه اجرایی ضرب ماتریس از $ O(n^3)$ به $ O(n^{2.8}) $ کاهش پیدا می‌کند که در ماتریس‌هایی با ابعاد بزرگ منجر به افزایش سرعت چشمگیری میشود.
ضرب چندجملهایها و ضرب اعداد بسیار بزرگ
[برگرد بالا]
با استفاده از روش تقسیم و حل می‌توان روشی بهینه‌تر از ضرب عادی چندجملهایها برای آنها تعریف کرد. در این روش چندجملهایها به دو قسمت تقسیم شده و با استفاده از یک سری روابط، ضرب و جمع شده و نتیجه نهایی را می‌دهند. از همین روش با اندکی تغییر برای ضرب اعداد بسیار بزرگ هم می‌توان استفاده کرد که با اعمال آن، مرتبه ضرب از $ O(n^2)$ به $ O(n^{1.58})$ کاهش پیدا می‌کند.
مسئله کاشیکاری (فرش کردن صفحه شطرنجی با موزاییک‌های L شکل)
[برگرد بالا]
مسئله کاشیکاری از مسائل جالب طراحی الگوریتم است. در این مسئله از شما خواسته میشود سطح یک قطعه زمین را که به صورت صفحه شطرنج شبکه‌بندی شده است با استفاده از کاشی‌هایی با شکل L بپوشانید. به طوری که خانه خاصی از این شبکه خالی بماند. می‌توان فرض کرد خانه خالی برای باغچه یا حوضچه کوچکی کنار گذاشته شده است.
مسئله تنظیم جدول مسابقات (تورنمنت)
[برگرد بالا]
شما را مسئول تهیه جدول مسابقات تیم‌های فوتبال محله کرده‌اند! این بازی‌ها به صورت دوره‌ای بوده و هر تیمی باید با تمام تیم‌های دیگر بازی کند. در ضمن هر تیم در روز تنها می‌تواند یک بازی انجام دهد. برای تهیه جدول مسابقات به صورت بهینه - که مسابقات در کوتاهترین زمان ممکن برگزار شود - الگوریتمی ابداع شده است که از روش تقسیم و حل استفاده می‌کند.
جستجوی دودویی
[برگرد بالا]
برای یافتن عنصری در یک آرایه نامرتب چاره‌ای نداریم جز این که از روش جستجوی خطی استفاده کنیم. در این روش از ابتدای آرایه شروع کرده و تک‌تک عناصر را بررسی میکنیم، تا زمانی که به عنصر دلخواه برسیم. بنابراین اگر آرایه مورد نظر $n$ عنصر داشته باشد، مرتبه اجرایی روش جستجوی خطی $ O(n) $ خواهد بود. اما در مورد آرایه مرتب روش دیگری نیز وجود دارد: روش جستجوی دودویی (Binary Search).
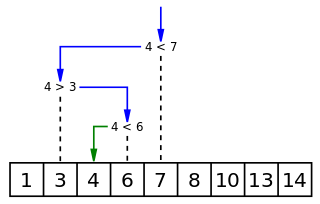
در جستجوی دودویی عنصر وسط آرایه را بررسی میکنیم. در صورتی که این عنصر همان عنصر مورد نظر باشد، جستجو تمام میشود. اگر نه، باید قسمت‌های راست و چپ عنصر وسط را که تقریبا به یک اندازه هستند مورد جستجو قرار دهیم. اما آیا لازم است هر دو سمت جستجو شود؟ چون آرایه مرتب شده است، عناصر کوچکتر از عنصر مرکز همگی در سمت چپ و عناصر بزرگتر در سمت راست آن قرار دارند (آرایه را مرتب شده صعودی در نظر گرفته‌ام). با توجه به این مسئله که عنصر مورد نظر ما کوچکتر از عنصر مرکزی آرایه است یا بزرگتر، تنها یکی از دو زیر آرایه را بررسی میکنیم. در نتیجه در هر مرحله بازه مورد جستجو نصف میشود.
برای یافتن مرتبه اجرایی الگوریتم به این صورت عمل میکنیم: فرض کنید $ T(n)$ حداکثر تعداد مقایسه‌های لازم برای یافتن عنصر مورد نظرمان در میان n داده باشد. در روش جستجوی خطی $T(n) = n$ بود. در روش جستجوی دودویی ابتدا عنصر وسط را با عنصر مورد نظرمان مقایسه میکنیم. اگر عنصر یافت نشود، در مرحله بعد تنها یکی از دو زیر آرایه بررسی میشود که نصف کل عناصر را دارد. پس می‌توان نوشت:
\[T(n) = T (\frac{n}{2}) + 1 \]
با حل این رابطه بازگشتی به عبارت زیر می‌رسیم:
\[T(n) = [log_2n] + 1 \]
که در آن منظور از [] علامت جزء صحیح است. مرتبه اجرایی این الگوریتم $ O(log \; n) $ است که در مقایسه با $ O(n) $ در جستجوی خطی بسیار کارآمد است. به عنوان نمونه، برای یافتن عنصری در یک آرایه به طول یک میلیون، در بدترین حالت با استفاده از جستجوی خطی یک میلیون مقایسه و در جستجوی دودویی تنها بیست مقایسه نیاز است.
نکته 1: ممکن است این سوال مطرح شود که هزینه مرتب کردن یک آرایه به مراتب بیشتر از هزینه جستجوی خطی است. چه لزومی به انجام این کار است؟ لیست قبول‌شدگان کنکور را در نظر بگیرید. این لیست پس از آماده شدن تنها یک بار بر اساس شماره داوطلبی مرتب شده و در سایت سازمان سنجش قرار می‌گیرد. پس از آن، طی چند روز میلیون‌ها مراجعه و جستجو در لیست برای مشاهده نتیجه صورت می‌گیرد. در این حالت مطمئنا هزینه چند میلیون جستجویی که انجام میشود، بسیار مهم‌تر از هزینه یک بار مرتب‌سازی آن است. بیشتر کاربردهای این روش جستجو هم در همین نوع داده‌ها است.
پیاده‌سازی الگوریتم‌های تقسیم و حل
[برگرد بالا]
در اکثر مواقع می‌توان الگوریتم‌های طراحی شده توسط روش تقسیم و حل را به صورت بازگشتی پیاده‌سازی کرد. چرا که هر کدام از زیرمسئله‌ها یک مسئله از همان نوع با پارامترهای متفاوت هستند.
در مورد جستجوی دودویی، پیاده‌سازی بازگشتی روش به زبان برنامه‌نویسی ++C به این ترتیب است:
int BinarySearch_1(int arr[], int left, int right, int x){
if(left > right){
return -1;
}
int m = (left + right) / 2, result;
if(arr[m] == x)
{
result = m;
}
else if(arr[m] > x){
result = BinarySearch_1(arr, left, m - 1, x);
}
else{
result = BinarySearch_1(arr, m + 1, right , x);
}
return result;
}
تابع فوق چهار پارامتر arr (آرایه‌ای که جستجو در آن انجام میشود)، left و right (مرزهای محدوده‌ای که جستجو باید در آن انجام شود) و x (عنصری که باید پیدا کنیم) را دریافت کرده و اندیس محلی که عنصر مورد نظر یافت شده بر می‌گرداند. به عنوان مثال اگر به دنبال عدد 78 در آرایه arr به طول هزار هستیم، باید تابع را به صورت زیر فراخوانی کنیم:
i = BinarySearch_1(arr, 0, 999, 78);
مقدار i پس از بازگشت از تابع برابر اندیس محل عنصر 78 در آرایه خواهد بود. اگر این عنصر یافت نشود مقدار 1- بازگشت داده میشود.
روش جستجوی دودویی پیاده‌سازی غیربازگشتی ساده‌تری هم دارد:
int BinarySearch_2(int arr[], int n, int x)
{
int left = 0, right = n - 1, m;
while(left <= right){
m = (left + right) / 2;
if (arr[m] == x){
return m;
}
if(arr[m] > x){
right = m - 1;
}
else{
left = m + 1;
}
}
return -1;
}
که در آن n تعداد عناصر آرایه است. مسلما سرعت اجرای این روش بیشتر از روش بازگشتی آن است. اما همیشه اینگونه نیست که پیاده‌سازی غیربازگشتی یک تابع سریعتر از پیاده‌سازی بازگشتی آن باشد.
نکته 2: در معرفی روش تقسیم و حل عنوان کردم که اگر زیرمسئله به اندازه کافی کوچک باشد از این روش برای حل آن استفاده نمی‌کنیم. تعیین این اندازه - که به آن مقدار آستانه گویند - بر اساس روش طراحی الگوریتم و همینطور روش‌های دیگر موجود صورت می‌گیرد که بحث مفصلی را می‌طلبد.
نکته 3: زمانی که مسئله را به چند زیرمسئله تقسیم میکنیم، اگر تقسیم طوری باشد که هر زیرمسئله خودش نزدیک به n ورودی داشته باشد، الگوریتم کارا نخواهد بود. نمونه چنین مسائلی محاسبه بازگشتی جمله nام
دنباله فیبوناتچی است.