سینوس و کسینوس را قورت بده

یکی از چالش‌های مهم دوران دبیرستان به یاد داشتن مقدار سینوس و کسینوس زوایای مشهور بوده و هست. در این راستا روش‌هایی مانند محاسبه به کمک دست و تا کردن انگشتان پیشنهاد شده است که هر کدام از انگشتان نماد یک زاویه هستند. اما چنین روش‌هایی خود نیازمند به یاد داشتن قوانین آن است که باعث بالا رفتن احتمال خطا می‌شود.

جدول زیر الگوی ساده موجود در مقدار سینوس و کسینوس زوایای مشهور را نشان می‌دهد که به سادگی در ذهن می‌ماند.

  

  

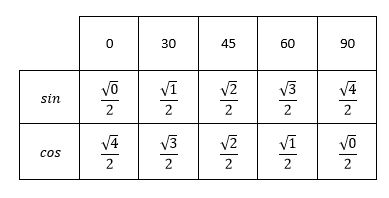
به عبارت دیگر سینوس صفر، سینوس 30، سینوس 45، سینوس 60 و سینوس 90 به ترتیب با قرار دادن اعداد صفر تا چهار در یک رابطه‌ی مشخص به دست می‌آید و همینطور برای کسینوس صفر، کسینوس 30، کسینوس 45، کسینوس 60 و کسینوس 90 از اعداد چهار تا صفر در همان رابطه استفاده می‌شود.

  

سینوس و کسینوس زاویه‌های 37 و 53

  [برگرد بالا]

به غیر از زوایای مشهور فوق، مقادیر سینوس و کسینوس دو زاویه‌ی 37 و 53 (که متمم هم هستند) نیز در مسائل زیاد استفاده می‌شوند. سینوس 37 (یا کسینوس 57) در دقت دو رقم اعشار عدد 0.6 و کسینوس 37 (یا سینوس 57) در دقت دو رقم اعشار 0.8 است

  

چرا سینوس 90 درجه یک است؟

  [برگرد بالا]

ما معمولا مفهوم سینوس و کسینوس یک زاویه را با مثالی از یک مثلث قائم‌الزاویه مانند تصویر زیر یاد می‌گیریم.

  

  

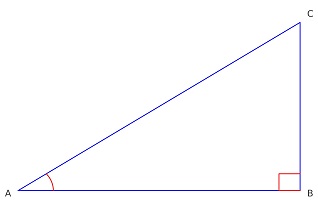
در این شکل سینوس زاویه‌ی A برابر نسبت طول ضلع روبرو بر طول وتر و کسینوس این زاویه برابر طول ضلع مجاور بر طول وتر است.

  

\[ sin(A) = \frac{|BC|}{|AC|} \] \[ cos(A) = \frac{|AB|}{|AC|} \]

  

با این تعریف چطور سینوس 90 محاسبه می‌شود؟ چطور ممکن است زاویه‌ی A هم 90 درجه باشد؟ سینوس زاویه‌ی 135 درجه چگونه محاسبه شده است؟ آیا می‌توان مثلثی رسم کرد که زاویه‌ی B قائم و زاویه‌ی A هم 135 درجه باشد؟ مجموع این دو زاویه بیش از 180 درجه است و قطعا نمی‌توان چنین مثلثی ساخت.

فرض کنید همان مثلث به صورت زیر در دستگاه مختصات دکارتی رسم شود.

  

  

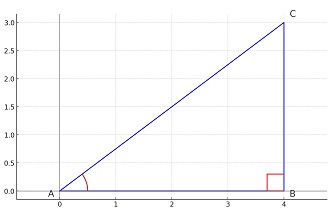
در نمایش زیر نقاط E و F تصویر نقطه‌ی C روی دو محور هستند . پس می‌توان از AF به جای BC و از AE به جای AB (که در اینجا یکی هستند) استفاده کرد. از طرف دیگر، چون A در مبدا مختصات قرار دارد، طول این تصویرها برابر موقعیت نقطه‌های انتهایی (یعنی E یا F) است.

  

  

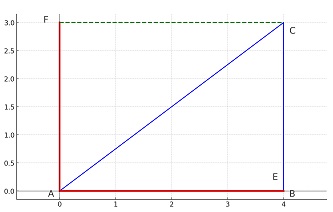
\[ sin(A) = \frac{|BC|}{|AC|} = \frac{|AF|}{|AC|} = \frac{F}{|AC|}\] \[cos(A) = \frac{|AB|}{|AC|} = \frac{|AE|}{|AC|} = \frac{E}{|AC|} \]

  

حال فرض کنیم A یک زاویه‌ی منفرجه باشد.

  

  

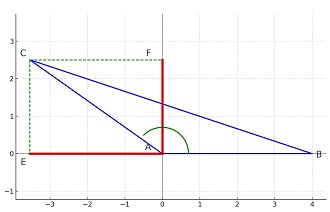
و به این ترتیب باز هم می‌توانیم تصویر AC را روی دو محور به دست آورده و از آنها برای محاسبه‌ی سینوس و کسینوس این زاویه استفاده کنیم.

  

\[ sin(A) = \frac{F}{|AC|} > 0\] \[ cos(A) = \frac{E}{|AC|} < 0 \]

  

به عبارت دیگر، برای محاسبه‌ی سینوس و کسینوس یک زاویه، نیاز نیست حتما یکی از زاویه‌ها 90 درجه باشد و چون ممکن است F یا E در سمت منفی محورشان باشند، عدد سینوس یا کسینوس نیز قابلیت منفی شدن دارند. با تعریف اولیه‌ای که بر اساس تقسیم طول ضلع بر طول وتر بود (تقسیم دو عدد همواره نامنفی)، میزان سینوس یا کسینوس هرگز منفی نمی‌شود.

به همین ترتیب اگر اندازه‌ی زاویه‌ی A برابر 90 درجه باشد، اندازه‌ی AC با تصویر خود روی محور عمودی (یعنی AF) یکی شده و اندازه‌ی تصویر آن روی محور افقی صفر می‌شود (چرا؟!).

  

  

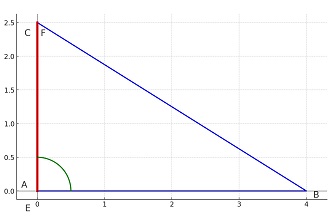
به همین دلیل سینوس 90 درجه یک و کسینوس 90 درجه صفر است.

  

\[ sin(90) = \frac{F}{|AC|} = \frac{C}{|AC|} = 1 \] \[cos(90) = \frac{E}{|AC|} = \frac{0}{|AC|} = 0 \]

  

دایره مثلثاتی

  [برگرد بالا]

اگر در مثال بالا طول AB و AC در مثلث هر دو یک باشند، می‌توان مثلث را در یک دایره به شعاع یک محصور کرد. به این دایره که شعاع آن یک است دایره‌ی واحد یا دایره‌ی مثلثاتی گفته می‌شود.

  

  

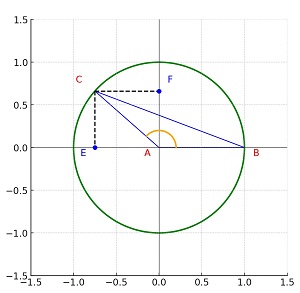
در چنین مثلثی چون طول AC یک است، روابط محاسبه‌ی سینوس و کسینوس خلاصه‌تر می‌شود.

  

\[ sin(A) = \frac{F}{|AC|} = \frac{F}{1} = F \] \[ cos(A) = \frac{E}{|AC|} = \frac{E}{1} = E \]

  

نکته‌ی دیگری که در محاسبات سینوس و کسینوس وجود دارد این است که این مقادیر وابسته به نقطه‌ی B نیستند و می‌توان از رسم آن صرف نظر کرد. پس دایره‌ی مثلثاتی به صورت خلاصه‌تر زیر هم قابل ترسیم است.

  

  

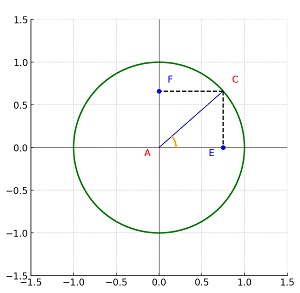
حال اگر خطوط مماس به دایره و موازی با محورها را رسم کنیم، محل تقاطع AC با آنها مقدار تانژانت و کتانژانت زاویه را مشخص می‌کند. این موضوع را می‌توان با توجه به قضیه تالس در مورد تناسب مثلث‌ها اثبات کرد.

  

  

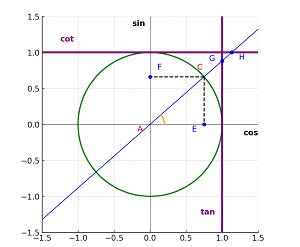
\[ tan(A) = \frac{sin(A)}{cos(A)} = \frac{F}{E} = G \] \[ cot(A) = \frac{cos(A)}{sin(A)} = \frac{E}{F} = H \]

  

همانگونه که در تصویر فوق مشخص شده است، در دایره‌ی مثلثاتی محور x محور کسینوس، محور y محور سینوس، خط مماس موازی با محور y محور تانژانت و خط مماس موازی با محور x محور کتانژانت نامگذاری می‌شوند. در واقع برای هر زاویه A محل E (تصویر AC روی محور کسینوس) مقدار کسینوس، محل F (تصویر AC رو محور سینوس) مقدار سینوس، محل G (تقاطع AC با محور تانژانت) مقدار تانژانت و محل H (تقاطع AC با محور کتانژانت) هستند.

در دایره‌ی مثلثاتی به وضوح مشخص است که هر چه زاویه‌ی A به سمت 90 درجه حرکت کند، مقدار سینوس به یک، مقدار کسینوس به صفر، مقدار تانژانت به بینهایت و مقدار کتانژانت نیز به صفر میل خواهند کرد. به همین ترتیب هر چه زاویه به صفر نزدیک شود، مقادیر سینوس، کسینوس، تانژانت و کتانژانت به ترتیب به صفر، یک، صفر و بینهایت میل می‌کنند. در حالت کلی هم مقادیر سینوس و کسینوس هر زاویه بین منفی یک تا یک متغیر است، اما مقادیر تانژانت و کتانژانت ممکن است هر عددی باشند.