ساختمان جدید دپارتمان مهندسی کامپیوتر تنها شامل آسانسور بوده و پله ندارد. برای دسترسی سریع و مناسب به اتاقها و کلاسهای طبقات مختلف، آسانسورها به گونهای تنظیم شدهاند که تنها در طبقات مشخصی توقف داشته باشند؛ مثلا تعدادی تنها در طبقات زوج و تعدادی دیگر تنها در طبقات فرد. دکمههای داخل آسانسور و کنار ورودی آسانسور نیز تنها برای همین طبقات از پیش مشخص شده فعال هستند.
این ایده دسترسی سریع و مناسب به طبقات ساختمان را برای برخی افراد فراهم میکند. به عنوان نمونه اعضای هیئت علمی دسترسی مستقیم به طبقات اتاقهای خود دارند. اما در حالت کلی باعث سردرگمی میشود. اگر شخصی بخواهد از طبقهای به طبقه دیگری برود، ممکن است هیچ آسانسوری در هر دوی آنها توقف نداشته باشد و شخص مجبور به تعویض آسانسور گردد. در چنین شرایطی این سوال پیش میآید که کدام آسانسور (یا آسانسورها) باید انتخاب شوند و کدام انتخابها شخص را در زمان کمتری به مقصد میرساند. اگر مسیر حرکت شخص از طبقه i به طبقه j به صورت $ i = f_1 \rightarrow f_2 \rightarrow f_3 \rightarrow \cdots \rightarrow f_k = j $ نمایش داده شود، عبارت $ \sum_{r=1}^{k-1} \vert f_i - f_{i+1} \vert $ زمان لازم برای رسیدن به مقصد از طریق آن مسیر است. برنامهای بنویسید که افراد را در استفاده بهتر (در زمان کمتر) از آسانسورها یاری کند.
[برگرد بالا]
هر ورودی از یک سطر با سه عدد i، n و j شروع میشود که به ترتیب تعداد آسانسورها، طبقه مبدأ و طبقه مقصد را مشخص میکند. در ادامه، طبقات توقف هر آسانسور در یک سطر مجزا آمده است که هر کدام با عدد m برای مشخص شدن تعداد طبقات توقف شروع میشوند.
n یک عدد طبیعی نابیشتر از 10 بوده و هر آسانسور حداکثر در 150 طبقه توقف میکند. انتهای ورودیها نیز سه عدد صحیح صفر برای i، n و j است.
2 2 5
5 0 1 3 5 7
5 0 2 4 6 8
3 3 8
6 0 1 2 3 4 5
5 0 6 7 8 9
4 0 4 5 6
0 0 0
[برگرد بالا]
به ازای هر ورودی تنها یک سطر شامل یک عدد در خروجی چاپ میشود که بیانگر حداقل زمان لازم برای جابجایی بین دو طبقه مشخص شده در ورودی مسئله است.
7
5
منبع: مسابقه ACM منطقهای آسیا 2014 - سایت تهران -
مسئله Elevators
[برگرد بالا]
[برگرد بالا]
طبقات و مسیرهایی بین آنها را میتوان با استفاده از گراف مدلسازی کرد. به این ترتیب که هر طبقه یک گره و ارتباطات بین طبقات با یال مشخص میگردد. برای ساختن این گراف، تمامی گرههای متناظر هر طبقه توقف آسانسور به سایر گرههای متناظر طبقات دیگر همان آسانسور متصل میشوند. وزن هر یال نیز برابر اختلاف طبقات گرههای متناظر آنهاست. با توجه به آنکه هزینه بالا رفتن و پایین آمدن یکی بوده و محدودیتی برای حرکت به سمت بالا یا پایین وجود ندارد، یالها بدون جهت و با وزن مثبت در نظر گرفته میشوند. به عنوان مثال، گراف متناظر ورودی نمونه دوم مسئله به این ترتیب خواهد شد:
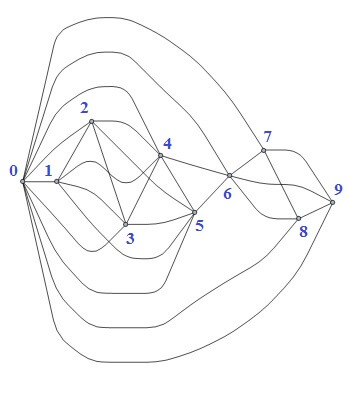
با توجه به این مدلسازی، حل مسئله تبدیل به یافتن کوتاهترین مسیر از گره طبقه مبدأ به گره طبقه مقصد میشود. پس میتوان با استفاده الگوریتم دایکسترا با مرتبه زمانی $O(n^2)$ به نتیجه مطلوب رسید.
نکته: الگوریتم فلوید-وارشال راهکار دیگری است که با مرتبه زمانی $\theta(n^3)$ کوتاهترین مسیر بین تمامی گرههای گراف را محاسبه میکند. در این مسئله هدف یافتن کوتاهترین مسیر بین دو گره مشخص (و نه تمامی گرهها) است. بنابراین نیازی به استفاده از الگوریتم فلوید-وارشال با مرتبه بدتر از الگوریتم دایکسترا احساس نمیشود. اما با توجه به اندازه حد آستانه مقادیر ورودی مسئله، این الگوریتم نیز در زمان مناسب به جواب میرسد. مزیت الگوریتم فلوید-وارشال نسبت به الگوریتم دایکسترا پیادهسازی آسان و سریع آن است.