جناب خان که با کسب و کار لبوی خود میلیاردر شده است، میخواهد رئیس جمهور شود! در کشور او که از چندین ایالت تشکیل شده است، از روشی با عنوان هیئت انتخاب (یا هیئت الکترال) برای انتخاب رئیس جمهور استفاده میشود.
در چنین ساختاری شمارش رأی در هر ایالت به صورت مستقل انجام میشود و هر ایالت متناسب با جمعیت خود تعدادی نماینده در هیئت انتخاب کنندگان رئیس جمهور دارد. تمام نمایندگان یک ایالت در نهایت به نامزدی رأی میدهند که در آن ایالت اکثریت آرا را کسب کرده باشد. اگر نامزدها رأی برابر داشته باشند، هر ایالت قوانین خاص خود برای انتخاب نهایی را دارد. در نهایت رئیس جمهور کسی است که بیش از نصف مجموع رأیهای هیئت انتخاب را از آن خود کند.
با در اختیار داشتن احتمال پیروزی جناب خان در هر ایالت، احتمال پیروزی وی در انتخابات را محاسبه کنید.
[برگرد بالا]
هر دسته ورودی با عدد n ($1 \leq n \leq 1000$) آغاز میشود که نشانگر تعداد ایالتها است. در ادامه n سطر شامل دو عدد آمده است که اعداد سطر i-ام احتمال پیروزی جناب خان در ایالت i-ام و تعداد نمایندگان آن ایالت در هیئت انتخاب است. تعداد کل نمایندگان همواره یک عدد فرد است و از 2000 بیشتر نیست.
انتهای ورودی با عدد صفر مشخص میشود.
1
0.4 1
3
0.5 1
0.5 2
0.5 10
3
0.5 1
0.5 2
0.5 2
2
0.2 1
0.8 10
2
0.25 1
0.751 10
0
[برگرد بالا]
به ازای هر ورودی احتمال پیروزی جناب خان در انتخابات با دقت دقیقا چهار رقم اعشار در یک سطر مجزا چاپ شود.
0.4000
0.5000
0.5000
0.8000
0.7510
منبع: مسابقه برنامهنویسی ICPC منطقهای سایت تهران 2016 -
مسئله Elections
[برگرد بالا]
دادههای مسئله شامل اطلاعات ایالتهای مختلف است که میتوان به صورت یک مجموعه در نظر گرفت. ایالتهایی با رأی حداکثر به جناب خان نیز زیرمجموعهای از این مجموعه است. حال سوال اینجاست که احتمال وقوع هر زیرمجموعه چقدر است و در کل چقدر احتمال دارد این زیرمجموعه شامل ایالاتی باشد که مجموع الکترالهای آنها بیش از نصف کل باشد.
نمونه ورودی سوم را در نظر بگیرید:
3
0.5 1
0.5 2
0.5 2
در این ورودی 5 نماینده وجود دارد و اگر نامزدی بتواند 3 رأی یا بیشتر جمع کند برنده است. اگر ایالتها را به ترتیب ورودی از 1 تا 3 شمارهگذاری کرده و احتمال برد جناب خان در ایالت i-ام را با $p_i$ نشان دهیم، در یکی از حالتهای زیر جناب خان برنده انتخابات خواهد بود:
1- جناب خان رأی ایالتهای 1 و 2 را داشته و رأی ایالت 3 را نداشته باشد که در مجموع 3 رأی الکترال خواهد داشت:
\[ p_1 \times p_2 \times (1 - p_3) = 0.5 \times 0.5 \times 0.5 = 0.125 \]
2- جناب خان رأی ایالتهای 1 و 3 را داشته و رأی ایالت 2 را نداشته باشد که در مجموع 3 رأی الکترال خواهد داشت:
\[ p_1 \times (1 - p_2) \times p_3 = 0.5 \times 0.5 \times 0.5 = 0.125 \]
3- جناب خان رأی ایالتهای 2 و 3 را داشته و رأی ایالت 1 را نداشته باشد که در مجموع 4 رأی الکترال خواهد داشت:
\[ (1 - p_1) \times p_2 \times p_3 = 0.5 \times 0.5 \times 0.5 = 0.125 \]
4- جناب خان رأی هر سه ایالت را داشته باشد که در مجموع 5 رأی الکترال خواهد داشت:
\[ p_1 \times p_2 \times p_3 = 0.5 \times 0.5 \times 0.5 = 0.125 \]
مجموع این احتمالات همان خروجی مورد نظر ما است:
\[ 0.125 + 0.125 + 0.125 + 0.125 = 0.5 \]
با کمی دقت مشخص است که هر حالت فوق مانند ساخت زیرمجموعهای از مجموعه کل ایالتها است. در حالت اول دو ایالت 1 و 2، در حالت دوم دو ایالت 1 و 3، در حالت سوم دو ایالت 2 و 3 و در حالت چهارم تمام ایالتها انتخاب شدهاند. دلیل عدم انتخاب سه زیرمجموعه غیر تهی دیگر (هر کدام از ایالتها به تنهایی) آن است که الکترال آنها به حد نصاب لازم نمیرسید.
بر اساس توضیحات فوق مشخص است که در بدترین حالت نیاز به انجام محاسبات فوق به ازای تک تک زیرمجموعههای غیر تهی مجموعه وجود دارد. اگر n بیانگر تعداد ایالتها باشد، تعداد زیرمجموعههای غیرتهی $ 2^n - 1 $ است که با توجه به حداکثر مقدار n، این محاسبه حتما بسیار بیشتر از زمان مورد انتظار برای حل مسئله طول میکشد.
با توجه به گسترده بودن فضای مسئله که از مرتبه نمایی است، باید سراغ راهکاری رفت که تعداد محاسبات را کم کند. مشکل اصلی نیز از آنجا ناشی میشود که محاسبات تکراری فراوانی وجود دارد.
این سوال بسیار مشابه مسئله کولهپشتی صفر و یک است که در آن تلاش میشود یک کولهپشتی با قدرت تحمل بار مشخص تا حد ممکن توسط مجموعهای از اشیاء با وزن و ارزش مشخص پر شود. در آن مسئله نیز هدف انتخاب زیرمجموعه بهینهای از اشیاء است که کوله را تا حد ممکن پر کند و از لحاظ ارزش نیز بهترین ترکیب را داشته باشد. این مسئله یک راهکار با روش برنامهنویسی پویا دارد که از مرتبه زمانی خطی است و میتوان از آن برای حل این مسئله الهام گرفت.
فرض کنیم n تعداد ایالتها، total تعداد کل نمایندگان در هیئت انتخاب و $t_i$ تعداد نمایندگان ایالت i-ام باشد. در این صورت کافی است یک آرایه دو بعدی با ابعاد $ (n + 1) \times (total + 1)$ بسازیم که عنصر سطر i و ستون j بیانگر انتخاب از ایالتها تا ایالت i-ام برای رسیدن به تعداد j نماینده است. در اینجا فرض کردهایم اندیس آرایه از صفر شروع میشود و سطر اول (اندیس صفر) بیانگر عدم انتخاب ایالتها است. بدیهی است در صورتی که هیچ ایالتی انتخاب نشود، احتمال موفقیت صفر و جناب خان بازنده است. همچین ستون اول (اندیس صفر) سطر j-ام بیانگر آن است که تا ایالت j-ام هیچ نمایندهای به نفع جناب خان انتخاب نشده باشد. مثلا برای سطر اول $ 1 - p_1 $ و برای سطر دوم $(1 - p_1)(1 -p_2)$ خواهد بود و الی آخر. بنا به این دو تفسیر، عنصر سطر اول و ستون اول همواره یک است (چرا؟). سایر عناصر ماتریس نیز با استفاده از رابطه زیر محاسبه میشوند:
\[ M[i][j] = \left \{ \begin{matrix} (1 - p_i) \times M[i - 1][j] + p_i \times M[i - 1][j - t_i] & & & j \geq t_i \\ (1 - p_i) \times M[i - 1][j] & & & j < t_i \end{matrix} \right. \qquad 1 \leq i, j \]
این محاسبات برای ورودی نمونه سوم در جدول زیر آمده است:
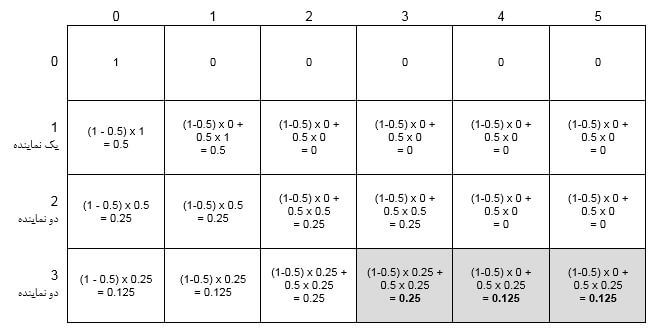
عدد ستون j-ام سطر آخر، احتمال رأی دادن j نماینده به جناب خان است. بنابراین اگر احتمال ستونهایی را که تعداد نمایندگان بیشتر از حد نصاب باشد (بخش رنگی در جدول بالا) جمع بزنیم، احتمال موفقیت جناب خان به دست میآید.
با استفاده از این راهکار مرتبه نمایی کل محاسبات به مرتبه $ O(total \times n) $ کاهش یافت که بر اساس حداکثر اندازه این دو متغیر در ورودی، خروجی نیز در زمان معقولی تولید میشود.
نکته: بر اساس روابط ذکر شده، هر سطر آرایه تنها بر اساس سطر قبلی خود ساخته میشود. هر عنصر در سطر نیز تنها وابسته به عناصر ستون خود یا قبل از خود در سطر قبلی است. با توجه به این نکنه نیازی به ذخیره کردن کل آرایه نیست و تنها با استفاده از یک آرایه یک بعدی نیز میتوان محاسبات را انجام داد (چگونه؟). در نتیجه حافظه مصرفی نیز کاهش پیدا میکند.