در علم کامپیوتر و ساختمان داده‌های برنامه‌نویسی منظور از درخت دودویی درختی است که از یک گره به نام ریشه و حداکثر دو زیردرخت برای این گره تشکیل شده است که هر کدام از این دو زیردرخت خودشان یک درخت دودویی هستند. به دو گره ریشه این دو زیردرخت (در صورت موجود بودن) فرزندان چپ و راست گفته می‌شود. به همین ترتیب زیردرختی که فرزند راست در گره آن قرار دارد زیردرخت راست و زیردرختی که فرزند چپ در گره آن قرار دارد زیردرخت چپ گره نامیده می‌شوند.
درخت جستجوی دودویی، درخت هیپ و درخت AVL سه نوع درخت دودویی هستند. آنچه این نوع درختها را از هم متمایز می‌کند روش ساخته شدن آنها یا نوع ارتباط معنایی بین گره‌های آنها است. به عنوان نمونه در یک درخت جستجوی دودویی مقدار تمام عناصر زیردرخت چپ هر گره از مقدار آن گره کوچکتر و مقدار تمام عناصر زیردرخت راست از آن بزرگتر هستند و در یک مکس هیپ مقدار هر گره از تمام مقادیر فرزندان خود بزرگتر یا مساوی است.
پیمایش درخت دودویی
[برگرد بالا]
هدف از پیمایش یک گراف دسترسی به تک تک گره‌های آن به منظور انجام عملیات مورد نظر (مانند جستجو) است. الگوریتم‌های پیمایش اول عمق و پیمایش اول سطح دو روش پرکاربرد پیمایش هر گراف دلخواه است که برای درختها به عنوان نوع ویژه‌ای از گراف‌ها نیز قابل استفاده هستند. پیمایش پیشوندی (پیش‌ترتیب یا PreOrder)، پیمایش میانوندی (میان‌ترتیب یا InOrder) و پیمایش پسوندی (پس‌ترتیب یا PostOrder) نیز سه نوع متداول پیمایش درخت دودویی هستند.
پیمایش میانوندی
[برگرد بالا]
تعریف بازگشتی پیمایش میانوندی یک درخت دودویی به این ترتیب است:
-
پیمایش زیردرخت چپ ریشه به روش میانوندی
-
پردازش ریشه
-
پیمایش زیردرخت راست ریشه به روش میانوندی
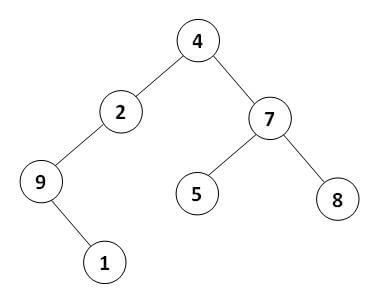
به عنوان نمونه برای درخت فوق نتیجه پیمایش میانوندی به این ترتیب خواهد شد:
9 1 2 4 5 7 8
کاربرد پیمایش میانوندی
[برگرد بالا]
مشهورترین کاربرد پیمایش میانوندی در درخت‌های جستجوی دودویی است. بر اساس تعریف درخت جستجوی دودویی اگر درخت با روش میانوندی پیمایش شود عناصر به صورت مرتب شده از کوچک به بزرگ پردازش می‌شوند. چرا که ابتدا زیردرخت چپ (همه عناصر کوچکتر از گره) سپس خود گره و در نهایت زیردرخت راست (همه عناصر بزرگتر از گره) پردازش می‌شود. پس هر گره از لحاظ ترتیب در جای درست قرار می‌گیرد. نمونه زیر یک درخت جستجوی دودویی و پیمایش میانوندی آن را نشان می‌دهد.
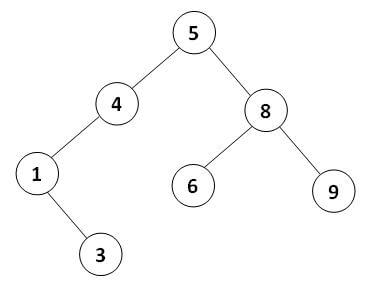
1 3 4 5 6 8 9
چنین پیمایشی یک ترتیب صعودی از عناصر درخت BST تولید می‌کند و اگر سه مرحله پیمایش را معکوس کنیم در نهایت به یک ترتیب نزولی می‌رسیم (چرا؟).
پیمایش پیشوندی
[برگرد بالا]
تعریف بازگشتی پیمایش پیشوندی یک درخت دودویی به ترتیب زیر است.
-
پردازش ریشه
-
پیمایش زیردرخت چپ ریشه به روش پیشوندی
-
پیمایش زیردرخت راست ریشه به روش پیشوندی
برای درخت فوق نتیجه پیمایش پیشوندی به این ترتیب خواهد شد:
4 2 9 1 7 5 8
در این نوع پیمایش خود گره در اولویت بیشتری نسبت به فرزندانش قرار دارد.
کاربرد پیمایش پیشوندی
[برگرد بالا]
یک کاربرد مهم پیمایش پیشوندی ساخت کپی از درخت است. بر اساس این نوع پیمایش همواره ریشه‌ای‌ترین گره در ابتدا و سپس فرزندان آن است و بنابراین می‌توان یک ساختار درخت مشابه درخت اصلی از بالا به پایین ساخت.
پیمایش پسوندی
[برگرد بالا]
تعریف بازگشتی پیمایش پسوندی یک درخت دودویی به ترتیب زیر است.
-
یمایش زیردرخت چپ ریشه به روش پسوندی
-
پبمایش زیردرخت راست ریشه به روش پسوندی
-
پردازش ریشه
به عنوان نمونه برای درخت فوق نتیجه پیمایش پسوندی به این ترتیب خواهد شد:
1 9 2 5 8 7 4
در این نوع پیمایش خود گره در اولویت آخر قرار دارد.
کاربرد پیمایش پسوندی
[برگرد بالا]
یک کاربرد پیمایش پسوندی در زمان حذف درخت است. چرا که بر اساس این نوع پیمایش همواره ریشه‌ای‌ترین گره در انتها پردازش می‌شود و قبل از آن تمام گره‌های زیردرخت‌های چپ و راست حذف می‌شوند. بنابراین می‌توان فضای اختصاص داده شده به درخت را با رویکرد پایین به بالا آزاد کرد. در مثال بالا نیز مشخص است که اگر قرار بر حذف کردن گره پردازش شده باشد، در هر مرحله یک برگ از درخت حذف می‌شود.
مرتبه زمانی الگوریتم‌های پیمایش درخت دودویی
[برگرد بالا]
در عملیات پیمایش یک گراف تمام گره‌های آن بازدید می‌شوند. بنابراین اگر $n$ بیانگر تعداد گره‌ها باشد، همواره $n$ عمل پردازش اطلاعات وجود دارد. اما بسته به نوع پیاده‌سازی ممکن است میزان حافظه مصرفی متفاوت باشد. پیاده‌سازی بازگشتی پیمایش‌های سه‌گانه فوق در زبان برنامه‌نویسی ++C به ترتیب زیر است که در آنها منظور از node یک ساختار تعریف شده به عنوان گره درخت است.
void preorder(node *root) {
if(!root)
return;
cout << "(" << root->info << ")";
preorder(root->Lchild);
preorder(root->Rchild);
}
void inorder(node *root) {
if(!root)
return;
inorder(root->Lchild);
cout << "(" << root->info << ")";
inorder(root->Rchild);
}
void postorder(node *root) {
if(!root)
return;
postorder(root->Lchild);
postorder(root->Rchild);
cout << "(" << root->info << ")";
}
در این نوع پیاده‌سازی تعداد فراخوانی‌های بازگشتی (که باعث مصرف حافظه می‌شود) به اندازه عمق درخت است. بنابراین مرتبه حافظه مصرفی بین $O(log_2 n)$ و $O(n)$ است. این مسئله در مورد پیاده‌سازی غیربازگشتی با استفاده از پشته نیز صدق می‌کند. اما قطعه کد زیر یک پیاده‌سازی غیربازگشتی بدون استفاده از پشته است که مقدار حافظه مصرفی آن مستقل از تعداد گره‌ها و عدد ثابتی است.
void preorder(node *root) {
node *curNode = root;
node *fromNode = NULL;
while(curNode) {
if(fromNode == curNode->parent) {
cout << "(" << curNode->value << ")";
fromNode = curNode;
if(curNode->left) {
curNode = curNode->left;
continue;
}
if(curNode->right) {
curNode = curNode->right;
continue;
}
curNode = curNode->parent;
}
else if(fromNode == curNode->left) {
fromNode = curNode;
if(curNode->right) {
curNode = curNode->right;
continue;
}
curNode = curNode->parent;
}
else {
fromNode = curNode;
curNode = curNode->parent;
}
}
}
void inorder(node *root) {
node *curNode = root;
node *fromNode = NULL;
while(curNode) {
if(fromNode == curNode->parent) {
fromNode = curNode;
if(curNode->left) {
curNode = curNode->left;
continue;
}
cout << "(" << curNode->value << ")";
if(curNode->right) {
curNode = curNode->right;
continue;
}
curNode = curNode->parent;
}
else if(fromNode == curNode->left) {
fromNode = curNode;
cout << "(" << curNode->value << ")";
if(curNode->right) {
curNode = curNode->right;
continue;
}
curNode = curNode->parent;
}
else {
fromNode = curNode;
curNode = curNode->parent;
}
}
}
void postorder(node *root) {
node *curNode = root;
node *fromNode = NULL;
while(curNode) {
if(fromNode == curNode->parent) {
fromNode = curNode;
if(curNode->left) {
curNode = curNode->left;
continue;
}
if(curNode->right) {
curNode = curNode->right;
continue;
}
cout << "(" << curNode->value << ")";
curNode = curNode->parent;
}
else if(fromNode == curNode->left) {
fromNode = curNode;
if(curNode->right) {
curNode = curNode->right;
continue;
}
cout << "(" << curNode->value << ")";
curNode = curNode->parent;
}
else {
fromNode = curNode;
cout << "(" << curNode->value << ")";
curNode = curNode->parent;
}
}
}
در این قطعه کدها تنها دو متغیر برای پیمایش کافی است و تعداد گره‌ها یا عمق درخت تاثیری در میزان حافظه مصرفی ندارند. متغیر curNode به گره جاری اشاره دارد و متغیر fromNode به گره ماقبل گره جاری (یعنی جایی که از آن به سمت گره جاری حرکت کردیم) اشاره می‌کند. این متغیر زمان حرکت به سمت برگ‌ها به والد گره اشاره می‌کند و زمان صعود به سمت ریشه درخت به یکی ار فرزندان گره. با مشخص بودن دو گره آخر پیمایش شده به راحتی می‌توان مسیر پیمایش را تشخیص داد.
نکته ۱: اگر همه عبارات چاپ گره پردازش شده از توابع فوق حذف شوند هر سه تابع دقیقا یک کد می‌شوند! ار این مسئله می‌توان به عنوان راهنمای روش کار و تحلیل الگوریتم استفاده کرد.
نکته ۲: اگر دو پیمایش مختلف از یک درخت دودویی موجود باشد، پیمایش سوم از طریق آنها قابل تولید است.