الگوریتمستان - پیچیدگی زمانی اجرای الگوریتم

زمانی که برای حل یک مسئله الگوریتم طراحی می‌کنیم یا قصد استفاده از یک الگوریتم از پیش ابداع شده را داریم، عموما برایمان مهم است بدانیم کارآیی الگوریتم چگونه است و تا چه حد می‌توان روی آن حساب باز کرد. به ویژه اگر برای حل یک مسئله بیش از یک الگوریتم موجود باشد، باید بتوان آنها را به نحوی با هم مقایسه کرد. گاهی چنین مقایسه‌ای بر اساس قابلیت پیاده‌سازی یا میزان سادگی پیاده‌سازی است. اما در بسیاری مواقع سرعت تولید خروجی الگوریتم بسیار مهمتر از پیچیدگی پیاده‌سازی یا مدت زمان مورد نیاز برای پیاده‌سازی است. به همین دلیل طراحی یک الگوریتم کارا بسیار مهم است و در مسابقات برنامه‌نویسی همچون ACM-ICPC نیز این توانایی محک می‌خورد. در کنار این موضوع، ممکن است میزان حافظه مورد نیاز هم مهم باشد.

  

  

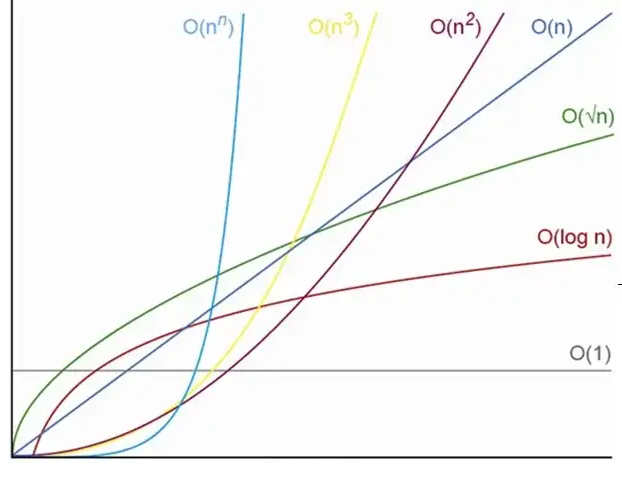
یک راه ساده برای مقایسه کارایی دو الگوریتم، پیاده‌سازی هر دو و بررسی زمان اجرا با ورودی‌های یک شکل است! این روش در عمل همواره ممکن نیست. دلیل اول آن است که در چنین حالتی باید سعی کنیم برنامه‌های الگوریتم‌ها را به بهترین حالت ممکن پیاده‌سازی کنیم و صرفا دغدغه کارایی الگوریتم را داشته باشیم. این شرط همواره مهم است و زمانی که کارایی دو الگوریتم بررسی می‌شود، به شرط پیاده‌سازی درست آنها است. چرا که یک پیاده‌سازی بد نتیجه استفاده از الگوریتم خوب را از بین می‌برد. اما هر پیاده‌سازی همواره با ابهام بهینه بودن همراه است و نمی‌توان مطمئن بود بهترین پیاده‌سازی ممکن است. مخصوصا اگر الگوریتم مورد نظر پیچیده باشد. از سوی دیگر، به صرف چند ورودی مشخص و نتایج آنها نمی‌توان از عملکرد کل الگوریتم مطمئن شد. ممکن است برای یک ورودی کوچک و حتی نه چندان کوچک یک الگوریتم بهتر از دیگری اجرا شود و اگر اندازه ورودی بزرگتر شود، نتیجه برعکس گردد یا حتی تغییرات متناقضی داشته باشند. یا آنکه ممکن است به ازای برخی ورودی‌ها زمان بسیار زیادی برای تولید خروجی نیاز باشد که در عمل آن میزان انتظار مقرون به صرفه نیست.

یک نکته کلیدی در مورد الگوریتم‌ها آن است اساسا الگوریتم‌ها ماهیتی مستقل از سخت‌افزار، زبان برنامه‌نویسی مورد استفاده جهت پیاده‌سازی و همینطور نحوه پیاده‌سازی دارند و تا حد ممکن باید سعی شود معیاری برای مقایسه یا تخمین کارایی استفاده شود که مستقل از این موارد باشند.

  

مفهوم پیچیدگی زمانی

  [برگرد بالا]

یک روش برآورد کارایی الگوریتم، شمارش تعداد عملیات اصلی مورد نیاز تا رسیدن به خروجی است. قطعه کد ساده زیر را در نظر بگیرید که مجموع اعداد $1$ تا $n$ را محاسبه می‌کند.

  

  

اگر خط اول کد را بخش اول، سه بخش حلقه for را بخش‌های دو تا چهار و خط بدنه حلقه را بخش پنجم در نظر بگیریم، بخش یک و دو تنها $1$ بار، بخش سه $ n + 1 $ بار و بخش‌های چهار و پنج هر کدام $n$ بار اجرا می‌شوند. پس در مجموع $3n+3$ عمل جمع، ضرب، مقایسه یا انتساب انجام می‌شود.

نکته: در محاسبه فوق بخش پنجم را یک عملیات در نظر گرفتیم که ترکیبی از عملیات جمع و انتساب است. همچنین در محاسبه تعداد عملیات، نوع هر عمل را در نظر نگرفتیم و فرض کردیم همه (جمع و ضرب و مقایسه و انتساب) به یک مقدار زمان جهت اجرا نیاز دارند. در ادامه می‌بینیم که در سطح ساده محاسبات پیچیدگی زمانی، اینطور فرضیات مشکلی ایجاد نمی‌کنند.

آنچه که در تحلیل عملکرد الگوریتم برای ما اهمیت دارد، میزان تغییر عملیات اصلی با بزرگ شدن اندازه ورودی است. مثلا اگر اندازه ورودی را $10$ برابر کردیم، چند برابر بیشتر باید منتظر تولید خروجی نسبت به حالت اولیه باشیم؟ در چنین شرایطی می‌توانیم از هر پارامتری که مستقل از اندازه ورودی مسئله است صرف نظر کنیم. مثلا در عبارت $3n+3$ جمع شدن با عدد $3$ امری مستقل از میزان بزرگی $n$ است و برای مقادیر بزرگ $n$ نیز این جمع تغییر چندانی در عدد نهایی ایجاد نمی‌کند. پس می‌توان از این ضریب ثابت صرف نظر کرد و تنها $3n$ را در نظر گرفت.

قطعه کد دیگری در نظر بگیرید که تعداد اعمال اصلی آن $9n-2$ باشد. بر اساس توضیحات قبلی تحلیل کارآیی این تعداد عملیات با تحلیل $9n$ تفاوتی ندارد. وجه مشترک $3n$ و $9n$ آن است که رشد خطی بر اساس تغییر $n$ دارند. در رشد خطی میزان رشد عملیات اصلی مستقل از ضریب $n$ و برابر با میزان رشد اندازه ورودی است.

این تفاسیر نشان از آن دارد که می‌توان $3n$ و $9n$ را از یک خانواده پیچیدگی زمانی دانست. به همین دلیل نیز در بخش پنجم قطعه کد فوق، تعداد کل تکرار دو دستور جمع و انتساب را به جای $2n$ تنها $n$ در نظر گرفتیم. چون این دو از یک خانواده هستند و در نهایت ضریب را می‌توان کنار گذاشت. ساده‌ترین عضو این خانواده $n$ است که به عنوان نماینده خانواده مطرح می‌شود. این نماینده را می‌توان با یک نماینده دیگر مانند $n^2$ به جای چندجمله‌هایی همچون $n^2-1000$ مقایسه کرد و نتیجه گرفت الگوریتمی از خانواده اول برای حل یک مسئله کاراتر از الگوریتمی از خانواده دوم برای حل همان مسئله است. چون $10$ برابر شدن اندازه ورودی، تاثیر $10$ برابری در زمان تولید خروجی خانواده اول و تاثیر $100$ برابری در زمان تولید خروجی خانواده دوم دارد. هر کدام از این خانواده‌ها یک مرتبه زمانی اجرا (یا حافظه مصرفی) هستند که با عنوان پیچیدگی زمانی (یا حافظه مصرفی) نیز شناخته می‌شوند.

در یک چندجمله‌ای مانند $6n^3-7n^2+4n-2$ عبارتی از درجات مختلف $n$ وجود دارد. ما زمانی که در مورد پیچیدگی زمانی صحبت می‌کنیم، منظورمان برای مقادیر به اندازه کافی بزرگ ورودی است. اگرنه برای مقادیر کوچک، عموما تمام الگوریتم‌ها در زمان قابل قبولی خروجی را تولید می‌کنند و دغدغه‌ای از بابت کارایی الگوریتم نداریم. به همین دلیل در چنین عبارتی جمله با رشد بیشتر مؤثرترین بخش است و عبارت در آن مرتبه پیچیدگی قرار می‌گیرد. یعنی چندجمله‌ای $6n^3-7n^2+4n-2$ از خانواده $n^3$ است و عبارت $ \frac{1}{1000}2^n+1000n^{10} - 7n + 3$ از خانواده $2^n$.

ممکن است این سوال مطرح شود که نقش ضریب را چگونه می‌توان تفسیر کرد؟ طبیعتا اگر یک الگوریتم از مرتبه $n$ و الگوریتم دیگری از مرتبه $n^3$ باشد، الگوریتم اول بسیار کاراتر است. اگر هر دو از یک مرتبه باشند، این ضریب‌ها هستند که سرعت رسیدن به جواب را مشخص می‌کنند. اما اگر این دو الگوریتم روی دو سیستم مجزا اجرا شوند، ضرایب لزوما راهنمای درستی نخواهند بود. به عنوان مثال، دو الگوریتم را در نظر بگیرید که به ترتیب $10n$ و $100n$ عمل اصلی دارند و روی دو سیستم متفاوت اجرا می‌شوند که سرعت پردازش دومی $100$ برابر بیشتر است. در چنین حالتی الگوریتم دوم $10$ برابر سریع‌تر از الگوریتم اول به نتیجه می‌رسد! ولی باز هم وجه مشترک آن دو این است که $k$ برابر شدن اندازه ورودی، زمان تولید خروجی را نیز تقریبا $k$ برابر می‌کند. در مقابل، فرض کنید الگوریتم دوم $n^2$ عمل اصلی داشته باشد. اگر اندازه ورودی $1000$ برابر شود، زمان تولید خروجی الگوریتم اول در سیستم کندتر نیز $1000$ برابر خواهد شد. اما این زمان برای الگوریتم دوم $1$ میلیون برابر می‌شود که بالا بودن سرعت پردازنده سیستم اجرایی آن نیز چندان کمکی به تولید خروجی در زمان نزدیک به الگوریتم اول روی سیستم کندتر نمی‌کند.

تذکر: در محاسبات پیچیدگی زمانی الگوریتم، هر ضریبی ضریب نیست! اگرچه $n$ و $\frac{n}{2}$ از یک خانواده هستند؛ اما $2^n$ و $2^{\frac{n}{2}}$ دو خانواده جدا از همند. عبارت دوم را می‌توان به صورت $\sqrt{2}^n$ نوشت و میزان رشد آن دو را مقایسه کرد.

  

پیچیدگی زمانی در بهترین و بدترین حالت

  [برگرد بالا]

در قطعه کد قبلی هر اجرا تعداد مشخصی عمل اصلی وابسته به $n$ داشت. اما برنامه‌ها لزوما از چنین الگوریتم‌هایی ساخته نمی‌شوند. تابع زیر را در نظر بگیرید که در $n$ عنصر اول آرایه arr مقدار x را جستجو کرده و اندیس آن را باز می‌گرداند.

  

  

در فرآیند جستجو ممکن است عنصر مورد نظر در هر یک از خانه‌های آرایه باشد یا اصلا وجود نداشته باشد که مقدار $-1$ توسط تابع بازگردانده می‌شود. بنابراین نمی‌توان رابطه ثابت و مشخصی برای تعداد اعمال اصلی تعریف کرد. در چنین شرایطی می‌توان گفت بهترین حالت اجرا از مرتبه $1$ است و بدترین حالت آن از مرتبه $n$. مرتبه $1$ مستقل بودن زمان اجرا از اندازه ورودی را مشخص می‌کند. عنصر مورد نظر چه در ابتدای یک آرایه با $10$ عنصر باشد و چه در ابتدای یک آرایه با $10^{100}$ عنصر، یافتن آن تنها یک مقایسه نیاز دارد و در زمان ثابتی اتفاق می‌افتد.

  

پیچیدگی زمانی متوسط الگوریتم

  [برگرد بالا]

دو حالت بهترین و بدترین ممکن است کم اتفاق بیفتند. محاسبه مرتبه بدترین حالت این حسن را دارد که نهایت منابع یا زمان مورد نیاز را برآورد می‌کنیم. اما عموما اجرا به ازای ورودی‌های مختلف به این میزان زمان یا حافظه نیاز ندارد. به همین دلیل حالت متوسط اجرا نیز محاسبه می‌شود تا بدانیم به طور متوسط الگوریتم در چه پیچیدگی زمانی سیر می‌کند.
حالت متوسط اجرا را می‌توان از محاسبه امید ریاضی به دست آورد. در مورد تابع جستجوی خطی فوق، با احتمال $\frac{1}{n}$ تعداد $i$ مقایسه (مقایسه تا خانه $i$ آرایه) ما را به جواب می‌رساند و امید ریاضی به ترتیب زیر محاسبه می‌شود.

\[ 1 \times \frac{1}{n} + 2 \times \frac{1}{n} + 3 \times \frac{1}{n} + \cdots + n \times \frac{1}{n} = ( 1 + 2 + 3 + \cdots + n) \times \frac{1}{n} \] \[ = \frac{n(n+1)}{2} \times \frac{1}{n} = \frac{n + 1}{2} = \frac{n}{2} + \frac{1}{2}\]

پس الگوریتم جستجوی خطی به طور متوسط نیز از مرتبه $n$ است. هرچند ضریب $n$ نسبت به بدترین حالت کمتر است. این ضریب به صورت شهودی هم قابل درک است که به طور متوسط نصف عناصر جستجو می‌شوند.

یک مثال دیگر روش حل مسئله برج هانوی است. برای جابجا کردن $n$ دیسک از میله مبدأ به میله مقصد ابتدا نیاز است $n-1$ دیسک بالایی را به میله کمکی منتقل کرده، سپس دیسک بزرگ را به میله مقصد برده و در نهایت دیسک‌های موجود در میله کمکی را به میله مقصد منتقل کنیم. اگر $T(n)$ تعداد حرکات مورد نیاز برای حل کامل مسئله باشد، بر اساس این توضیح می‌توان نوشت:

\[ T(n) = T(n-1) + 1 + T(n-1) = 2T(n-1)+1, \quad T(1) = 1 \]

حل این رابطه بازگشتی به $T(n) = 2^n-1 $ می‌رسد. پس حل این مسئله از مرتبه پیچیدگی $2^n$ است. این مسئله بهترین و بدترین حالت ندارد و همواره یک رابطه برای آن برقرار است و نمی‌توان الگوریتم کاراتری نیز برای آن نوشت. پس می‌توان نتیجه گرفت به ازای مقادیر بزرگ $n$ حل آن بسیار زمانبر خواهد بود. به همین دلیل نیز از آن افسانه ساخته‌اند!

نکته آخر: در نوشته فوق همواره از ورودی‌های به اندازه کافی بزرگ بحث شده است. به عبارت دیگر ممکن است برای مقادیر کوچک ورودی، الگوریتمی با مرتبه بزرگتر بهتر جواب دهد. از سوی دیگر در برخی از مسائل اندازه ورودی محدودیت دارد و می‌توان برای آن حداکثر قائل شد. در چنین شرایطی ممکن است یک الگوریتم از مرتبه بزرگ هم کارایی خوبی داشته باشد. اگر پیاده‌سازی چنین الگوریتمی نیز ساده باشد، بهتر است از آن استفاده شود. نمونه‌ای از چنین مسائل مسئله آسانسورها از سوالات مسابقات برنامه‌نویسی ACM-ICPC است.